Предмет: Математика,
автор: mefody66
Еще одна 26 задача.
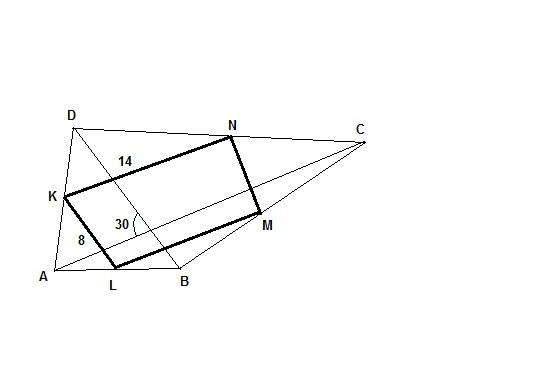
В выпуклом 4-угольнике ABCD середины сторон K, L, M, N.
KL = 8; KN = 14; угол между диагоналями (AC; BD) = 30°.
Всё показано на рисунке.
Найти площадь S(KLMN)
Приложения:
Ответы
Автор ответа:
0
в ΔADC KN - средняя линия => S(KDN) = S(ADC)/4 и AC = 2*14 = 28
в ΔABC LM - средняя линия => S(LBM) = S(ABC)/4
в ΔABAD LK - средняя линия => S(LAK) = S(BAD)/4 и BD = 2*8 = 16
в ΔDCB NM - средняя линия => S(NCM) = S(DCB)/4
S(ALK) + S(NCM) = S(ABCD)/4
S(KDN) + S(LMB) = S(ABCD)/4
S(ALK) + S(NCM) + S(KDN) + S(LMB) = S(ABCD)/2
S(KLMN) = S(ABCD) - (S(ALK) + S(NCM) + S(KDN) + S(LMB)) = S(ABCD)/2
S(ABCD) = 0,5 * AC * BD * sin30° = 0,5 * 28 * 16 * 0,5 = 14 * 8 = 112
S(KLMN) = 112/2 = 56
Ответ: 56
в ΔABC LM - средняя линия => S(LBM) = S(ABC)/4
в ΔABAD LK - средняя линия => S(LAK) = S(BAD)/4 и BD = 2*8 = 16
в ΔDCB NM - средняя линия => S(NCM) = S(DCB)/4
S(ALK) + S(NCM) = S(ABCD)/4
S(KDN) + S(LMB) = S(ABCD)/4
S(ALK) + S(NCM) + S(KDN) + S(LMB) = S(ABCD)/2
S(KLMN) = S(ABCD) - (S(ALK) + S(NCM) + S(KDN) + S(LMB)) = S(ABCD)/2
S(ABCD) = 0,5 * AC * BD * sin30° = 0,5 * 28 * 16 * 0,5 = 14 * 8 = 112
S(KLMN) = 112/2 = 56
Ответ: 56
Похожие вопросы
Предмет: Математика,
автор: hiimloveanime
Предмет: Українська мова,
автор: veronikashandrenko88
Предмет: Математика,
автор: makscheredadjg87
Предмет: Алгебра,
автор: ainurerkenovw
Предмет: Биология,
автор: ruhlovaolga