Предмет: Алгебра,
автор: vsemdratyti
Срочно на завтра!
Найти все тригонометрические функций числа x/2,если: (задания на фотке)
Приложения:
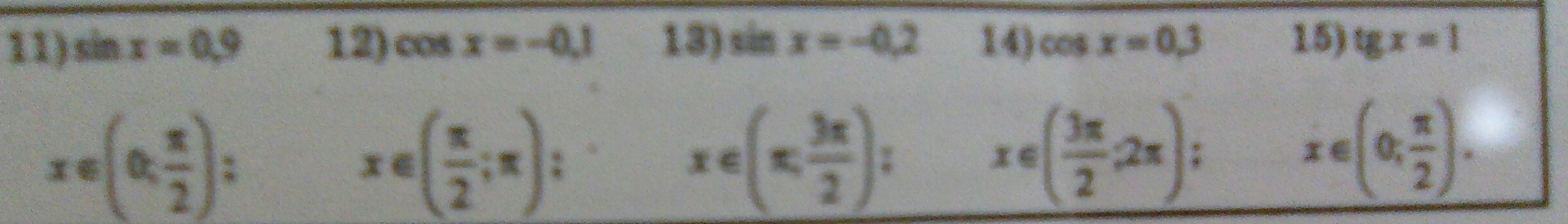
Ответы
Автор ответа:
0
11)sinx=0,9; (0;π/2) ----------> cosx>0;tgx>0;ctgx>0
2sin^2 (x/2)=1-cosx; sin^2 x+cos^2 x=1; cosx=+√(1-sin^2 x);
cosx=√(1-0,81)=√0,19
sin^2 (x/2)=(1-√0,19)/2; sin(x/2)=√(1-√0,19) /2=0,5√(1-√0,19)
tg(x/2)=(1-сosx)/(1+сcsx);
tg(x/2)=(1-√0,19) / (1+√0,19)=((1-√19)(1-√19)) /(1-19)=-1/18*(1-2√19+19)=
-1/18 *(20-2√19);ctgx/2=1/tg(x/2); ctgx/2=(1+√19) /(1-√19)=(20+2√19)/(-18)
12) cosx=-0.1 x⊂(π/2;π) ---->sinx>0; tgx<0; ctgx<0
cos^2 (x/2)=(1+cosx)/2; cos^2 x/2=(1-0,1);cos^2 (x/2)=0,9; cosx/2=-√0,9;
tgx/2=(1-√0,9) / (1+√0,9)=(1,9-2*√0,9)) /(0,1=10(1-2√0,9)
ctgx/2 = (1,+√0,9) /(1-√0,9)=(1,9+2√0,9) / (1-0,9)=10(1,9+2√0,9)
2sin^2 (x/2)=1-cosx; sin^2 x+cos^2 x=1; cosx=+√(1-sin^2 x);
cosx=√(1-0,81)=√0,19
sin^2 (x/2)=(1-√0,19)/2; sin(x/2)=√(1-√0,19) /2=0,5√(1-√0,19)
tg(x/2)=(1-сosx)/(1+сcsx);
tg(x/2)=(1-√0,19) / (1+√0,19)=((1-√19)(1-√19)) /(1-19)=-1/18*(1-2√19+19)=
-1/18 *(20-2√19);ctgx/2=1/tg(x/2); ctgx/2=(1+√19) /(1-√19)=(20+2√19)/(-18)
12) cosx=-0.1 x⊂(π/2;π) ---->sinx>0; tgx<0; ctgx<0
cos^2 (x/2)=(1+cosx)/2; cos^2 x/2=(1-0,1);cos^2 (x/2)=0,9; cosx/2=-√0,9;
tgx/2=(1-√0,9) / (1+√0,9)=(1,9-2*√0,9)) /(0,1=10(1-2√0,9)
ctgx/2 = (1,+√0,9) /(1-√0,9)=(1,9+2√0,9) / (1-0,9)=10(1,9+2√0,9)
Автор ответа:
0
спс
Похожие вопросы
Предмет: Қазақ тiлi,
автор: kuanyshaitbai8
Предмет: Математика,
автор: abelichev1705
Предмет: История,
автор: Vetta2461
Предмет: Химия,
автор: grait09