Question

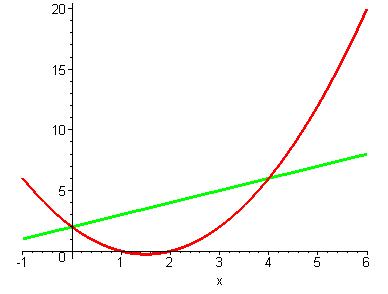
Обчислити площу фігури, обмеженої параболою y=x^2-3x+2 i прямою y=x+2

Answer 1

Фигура не ограничена ничем, кроме точек пересечения графиков. Найдём эти точки:

$x^2-3x+2=x+2\ x^2-4x=0\ x(x-4)=0\ begin{cases} x=0\ x=4 end{cases}\ y(0)=2\ y(4)=6\ A(0;;2)\ B(4;;6)$

x=0 и x=4 - пределы интегрирования.

График прямой x+2 находится выше графика параболы. 

Значит, площадь данной фигуры

$S=int_0^4((x+2)-(x^2-3x+2))dx=int_0^4(x+2-x^2+3x-2)dx=\=int_0^4(-x^2+4x)dx=left.left(-frac{x^3}3+2x^2right)right|_0^4=-frac{64}3+2cdot16+0-0=\=-21frac13+32=10frac23$