Question

В треугольнике со сторонами 13,12 и 14 см найти радиус описанной окружности и угол, противолежащий меньшей стороне

Answer 1

$R= dfrac{abc}{4S }$

По формуле Герона
$S= sqrt{p(p-a)(p-b)(p-c)} \ p= dfrac{13+12+14}{2}= 19,5 \ S= sqrt{19,5(19,5-13)(19,5-12)(19,5-14)}= \ =sqrt{19,5*6,5*7,5*5,5} = \ = sqrt{5227}=72,3 \ \ R= dfrac{12*13*14}{4*72,3}= dfrac{1820}{241}=7,6$

По теореме синусов
$dfrac{a}{sinA}=2R \ \ dfrac{12}{sinA}=15,2 \ \ sinA= dfrac{12}{15,2}=0,7894$

∠A=52°

Ответ: R=7,6; ∠A=52°

Answer 2

если можешь можешь 2 решить=) пж!

Answer 3

у меня же в вопросах

Answer 4

Можно вопросик откуда взялось 15,2?

Answer 5

Первое решение полное и понятное. Если  не помните формулу Герона, есть 

Вариант решения ( без формулы Герона). 

Формула радиуса описанной окружности 

R=a•b•c/4S, где а, b, и с - стороны треугольника

S-a•h

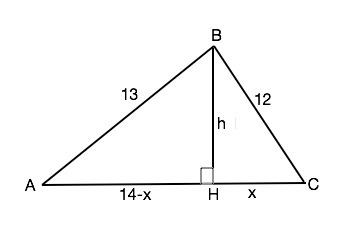
Проведем к большей стороне АС высоту ВН.

Примем СН=х

Тогда АН=14-х 

По т.Пифагора 

ВН²=АВ²-АН² =169-196+28х-х²

ВН²=ВС²-СН²=144-х²

Приравняем значения квадрата высоты:

169-196+28х-х²=144-х², откуда 

28х=171

х=6,107

ВН=√(144-37,3)=√106,7=10,33 

S=10,33•14/2=72,31

R=12•13•14/4•72,31=546/72,3= ≈7,55 см

sinA=BH/АВ==10,33/13= ≈0,7946

∠А≈52°36'