Question

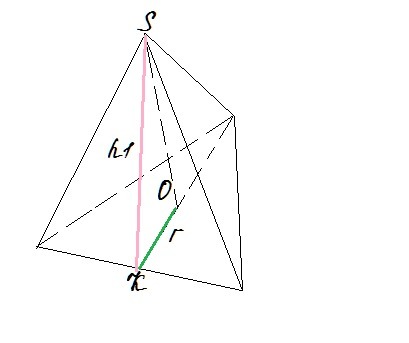
В правильной треугольной пирамиде Sбок=96√3,Sпол=112√3. Найдите сторону основания и высоту пирамиды.

Answer 1

Sосн = Sпол - Sбок = 16√3. Поскольку треугольная  пирамида правильная, то в основе лежит правильный треугольник. Следовательно, найдем сторону основания:
 $a= sqrt{ dfrac{4S_o}{ sqrt{3} } } = sqrt{ dfrac{4cdot 16 sqrt{3} }{ sqrt{3} } } =8$ - сторона основания.

Радиус вписанной окружности основания: r = a/2√3 = 4/√3

Площадь грани: Sграни = Sбок : 3 = 32√3, тогда высота грани 
h₁ = 2 * Sграни / a = 8√3

По т. Пифагора

h = √(h₁²-r²) = 4√105/3