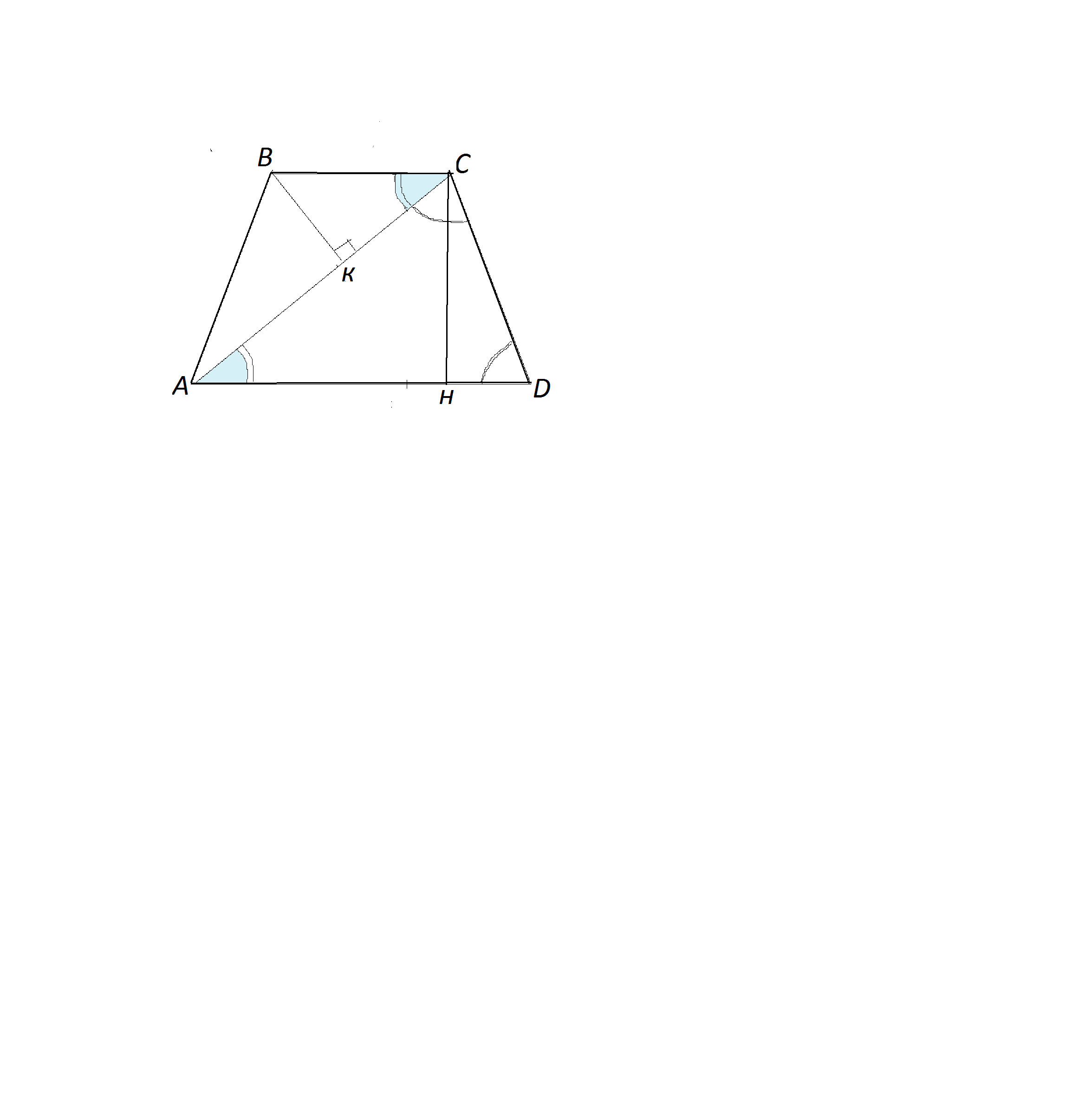
Найти расстояние от вершины B до диагонали AC,если основания AD и BC равнобедренной трапеции ABCD равны соответственно 10 см и 6 см,и диагональ AC равна 10 см.
Ответы
Сделаем рисунок к задаче.
Из вершины С опустим на большее основание высоту СН.
В равнобедренной трапеции высота, опущенная из тупого угла, делит основание на отрезки, больший из которых равен полусумме оснований, меньший - полуразности.
Отрезок АН основания АD равен полусумме оснований и равен
(10+6):2=8 см
Рассмотрим прямоугольные ⊿ АСН и ⊿ ВКС.
Углы САН и ВСК в них равны как накретслежащие при параллельных ВС и АD и секущей АС.
Если в прямоугольных треугольниках есть равные острые углы, то эти треугольники подобны.
Из ⊿ САН по т.Пифагора
СН=√9АС²- АН²)=√(100-64)=6 см
Из подобия ⊿ ВСК и ⊿ АСН
АС:ВС=СН:ВК
10:6=6:ВК
10 ВК=36 см
ВК=3,6 см
Ответ: Расстояние от вершины B до диагонали AС=3,6 см