Предмет: Алгебра,
автор: Kirina1
помогите, пожалуйста
Приложения:
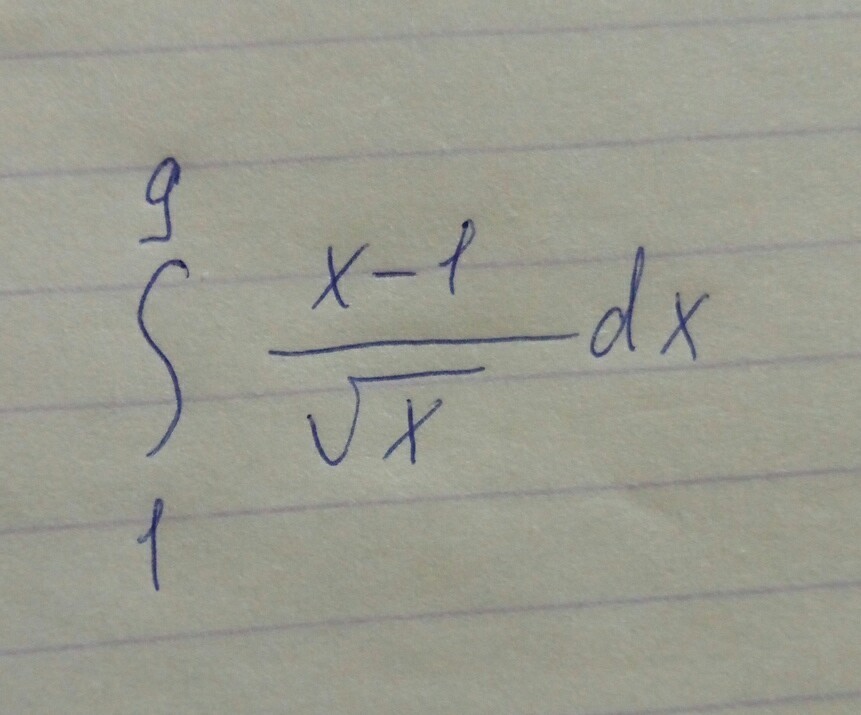
Ответы
Автор ответа:
0
Автор ответа:
0
Похожие вопросы
Предмет: Литература,
автор: popovaalisa153453
Предмет: Литература,
автор: annagryshko2018
Предмет: Українська мова,
автор: natapaleha81
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: krictinka23