Предмет: Геометрия,
автор: Аноним
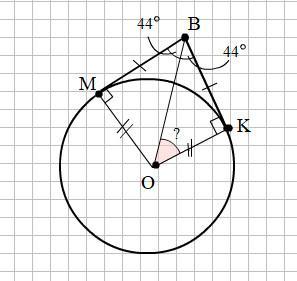
Из точки B к окружности с центром О проведены две касательные,K и M-точки касания.Известно, что ∠KBM=88°. Найдите ∠BOK.
Ответы
Автор ответа:
0
Ответ:
∠BOK = 46°
Объяснение:
Смотри прикреплённый рисунок.
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности, поэтому
∠ОВК = 0,5 ∠ КВМ = 0,5 · 88° = 44°.
ΔВОК - прямоугольный (∠ВКО = 90°, так как касательная ВК перпендикулярна радиусу ОК).
Сумма острых углов прямоугольного треугольника равна 90°
∠ВОК + ∠ОВК = 90°
∠ВОК = 90° - ∠ОВК = 90° - 44° = 46°
Приложения:
Похожие вопросы