Предмет: Геометрия,
автор: viktoria040602
ДАЮ 99 БАЛЛОВ, ПОМОГИТЕ, ПОЖАЛУЙСТА!
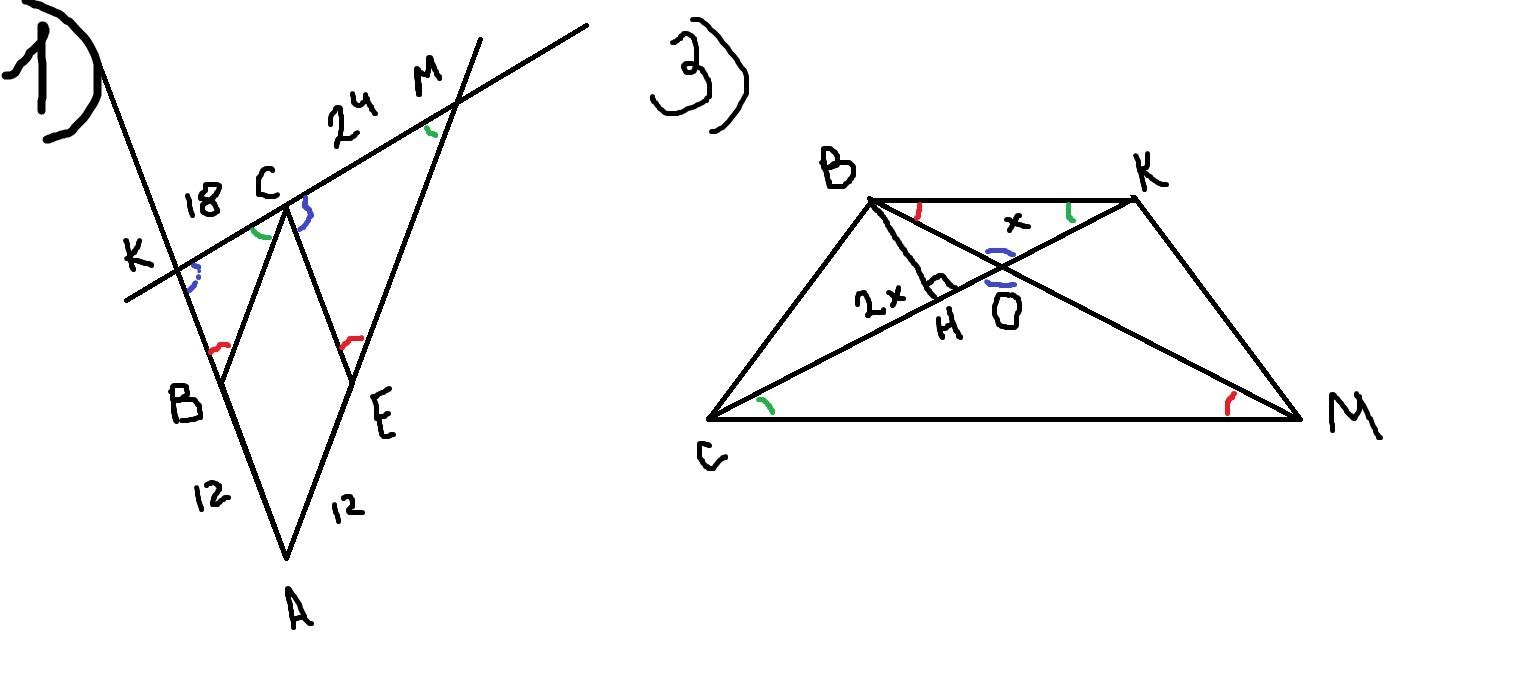
1. Сторона ромба ABCE равна 12. Прямая, проходящая через вершину С, пересекает продолжения сторон АВ и АЕ в точках К и М соответственно. Найдите периметр треугольника АКМ, если СК=18, СМ=24.
2. В прямоугольном треугольнике АВС с прямым углом С проведена биссектриса ВК. Найдите площадь треугольника АВК, если площадь треугольника АВС=21, а Sin∠A=0.4?
3. Диагонали трапеции СЕКМ (ЕК и СМ- основания) пересекаются в точке О. Площадь треугольника СОЕ равна 16, а СО=20К. Найдите площадь данной трапеции.
С ПОЛНЫМ РЕШЕНИЕМ, ПОЖАЛУЙСТА!!!!!!!!!!
Ответы
Автор ответа:
0
1)
CBK MEC - подобны по трем углам
BC/EM=BK/EC=CK/MC=18/24=3/4
BC/EM=3/4
EM=3/4 BC=4/3 *12=16
BK/EC=3/4
BK=3/4 * EC=3/4*12=9
P= AB+BK+CK+CM+EM+AE= 12+9+18+24+16+12=91
3)
KEO COM - подобны по трем углам
k=1/2 - коэффициент отношения
S(KEO)/S(COM)=k^2=1/4
S(CEM)=S(CKM)
S(CEO)+S(COM)=S(KOM)+S(COM)
S(CEO)=S(KOM)=16
S(CEO)=BH*CO
S(KEO)=BH*KO
S(CEO)/S(KEO)=CO/KO=2
S(KEO)=S(CEO)/2=8
S(KEO)/S(COM)=1/4
S(COM)=4S(KEO)=32
S(CEKM)=S(CEO)+S(KOM)+S(KEO)+S(COM)=16+16+8+32=72
CBK MEC - подобны по трем углам
BC/EM=BK/EC=CK/MC=18/24=3/4
BC/EM=3/4
EM=3/4 BC=4/3 *12=16
BK/EC=3/4
BK=3/4 * EC=3/4*12=9
P= AB+BK+CK+CM+EM+AE= 12+9+18+24+16+12=91
3)
KEO COM - подобны по трем углам
k=1/2 - коэффициент отношения
S(KEO)/S(COM)=k^2=1/4
S(CEM)=S(CKM)
S(CEO)+S(COM)=S(KOM)+S(COM)
S(CEO)=S(KOM)=16
S(CEO)=BH*CO
S(KEO)=BH*KO
S(CEO)/S(KEO)=CO/KO=2
S(KEO)=S(CEO)/2=8
S(KEO)/S(COM)=1/4
S(COM)=4S(KEO)=32
S(CEKM)=S(CEO)+S(KOM)+S(KEO)+S(COM)=16+16+8+32=72
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nurgaishakalikova
Предмет: Українська мова,
автор: borovoy06nik
Предмет: Алгебра,
автор: cebotarovailona
Предмет: Геометрия,
автор: Elizaveta080299
Предмет: Алгебра,
автор: TanyaZveginceva