Предмет: Алгебра,
автор: Roco95
Нужно решить систему неравенств.
Вторая строчка вроде бы получилась, а вот с первой проблемы. Степени двойки разложил. Вынес под одну с тройкой, а потом тупик. Если возможно, то помогите решить обе, заодно проверю. Заранее спасибо :)
Приложения:
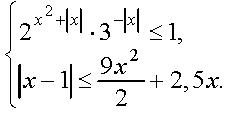
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: gumerpro333
Предмет: Алгебра,
автор: haimran102
Предмет: Математика,
автор: windyrainsun
Предмет: Геометрия,
автор: Adelinaria