Question

ребро куба ABCDA1B1C1D1 равно 3. найдите синус угла между плоскостями АВС и BDA1/

Answer 1

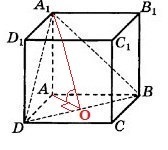
АВСDA1B1C1D1 - кукб.

АВСD - квадрат. => AO⊥BD. А1O⊥BD по теореме о трех перпендикулярах: прямая (BD), проведенная на плоскости (ABCD) через основание наклонной (А1О), перпендикулярна ее проекции (АО), то она перпендикулярна наклонной (А1О).

Двугранный угол, образованный полуплоскостями АВС и BDA1 измеряется величиной его линейного угла (<AOA1), получаемого при пересечении двугранного угла плоскостью (AOA1), перпендикулярной его ребру (BD).

Искомый угол <AOA1 = α, а его синус равен отношению противолежащего катета АА1 к гипотенузе А1О.

АА1=3 (дано), а АО = 3√2/2, как половина диагонали квадрата со стороной, равной 3.

Тогда по Пифагору А1О=√(АА1²+АО²) = 3√6/2.

Sinα = 3*2/(3√6) = 2/√6 = √6/3.