Предмет: Геометрия,
автор: Кентервильский1монах
Помогите!!!! Пожалуйста!!!
задачи 4 и 5 (на следующей странице)
Приложения:


Ответы
Автор ответа:
0
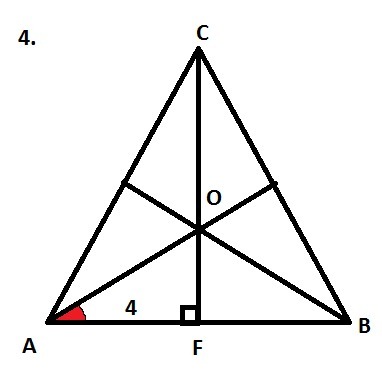
4.
1) О - точка пересечения медиан треугольника АВС, значит ΔАОВ, ΔВОС, ΔАОС - равновелики, т.е. имеют одинаковую площадь, значит S(ABC)=3*S(AOB).
2) Рассмотрим ΔАОВ, S(AOB)=1/2*AB*OF.
3) Рассмотрим ΔOAF - прямоугольный, AF=4 см, tg∠OAF=1/4=OF/AF, 1/4=OF/4, OF=1 см.
4) S(AOB)=1/2*AB*OF=1/2*8*1=4 (см²).
5) S(ABC)=3*S(AOB)=3*4=12 (см²).
Ответ: 12 см².
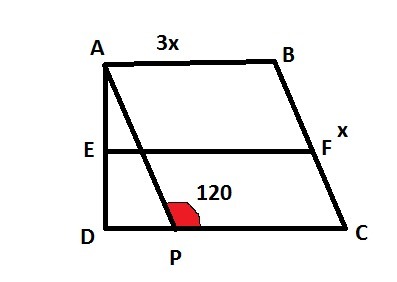
5.
1) Пусть EF - средняя линия трапеции ABCD, EF=(AB+DC)/2.
AB=3x, BC=x.
2) ABCP - параллелограмм (AB||DC - основания трапеции, AP||BC - по условию).
S(ABCP)=AB*BC*sin120°=6√3;
3x*x*√3/2=6√3;
3x²/2=6;
3x²=12;
x²=4;
x=2.
BC=2 см, АВ=PC=3*2=6 (см).
3) ΔADP - прямоугольный, АР=ВС=2 см, ∠АPD=60°, ∠DAP=30°⇒
DP=1/2*AP=1/2*2=1 (см).
DC=DP+PC=1+6=7 (см).
4) EF=(AB+DC)/2=(6+7)/2=13/2=6,5 (см).
Ответ: 6,5 см.
1) О - точка пересечения медиан треугольника АВС, значит ΔАОВ, ΔВОС, ΔАОС - равновелики, т.е. имеют одинаковую площадь, значит S(ABC)=3*S(AOB).
2) Рассмотрим ΔАОВ, S(AOB)=1/2*AB*OF.
3) Рассмотрим ΔOAF - прямоугольный, AF=4 см, tg∠OAF=1/4=OF/AF, 1/4=OF/4, OF=1 см.
4) S(AOB)=1/2*AB*OF=1/2*8*1=4 (см²).
5) S(ABC)=3*S(AOB)=3*4=12 (см²).
Ответ: 12 см².
5.
1) Пусть EF - средняя линия трапеции ABCD, EF=(AB+DC)/2.
AB=3x, BC=x.
2) ABCP - параллелограмм (AB||DC - основания трапеции, AP||BC - по условию).
S(ABCP)=AB*BC*sin120°=6√3;
3x*x*√3/2=6√3;
3x²/2=6;
3x²=12;
x²=4;
x=2.
BC=2 см, АВ=PC=3*2=6 (см).
3) ΔADP - прямоугольный, АР=ВС=2 см, ∠АPD=60°, ∠DAP=30°⇒
DP=1/2*AP=1/2*2=1 (см).
DC=DP+PC=1+6=7 (см).
4) EF=(AB+DC)/2=(6+7)/2=13/2=6,5 (см).
Ответ: 6,5 см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zeinelarsengo
Предмет: Математика,
автор: shullere
Предмет: Русский язык,
автор: viktoriakyprava
Предмет: Математика,
автор: azasyhina
Предмет: Математика,
автор: Кристя551