Предмет: Алгебра,
автор: GTR123321123
Непростой пример из профильного уровня ЕГЭ по математике
Приложения:
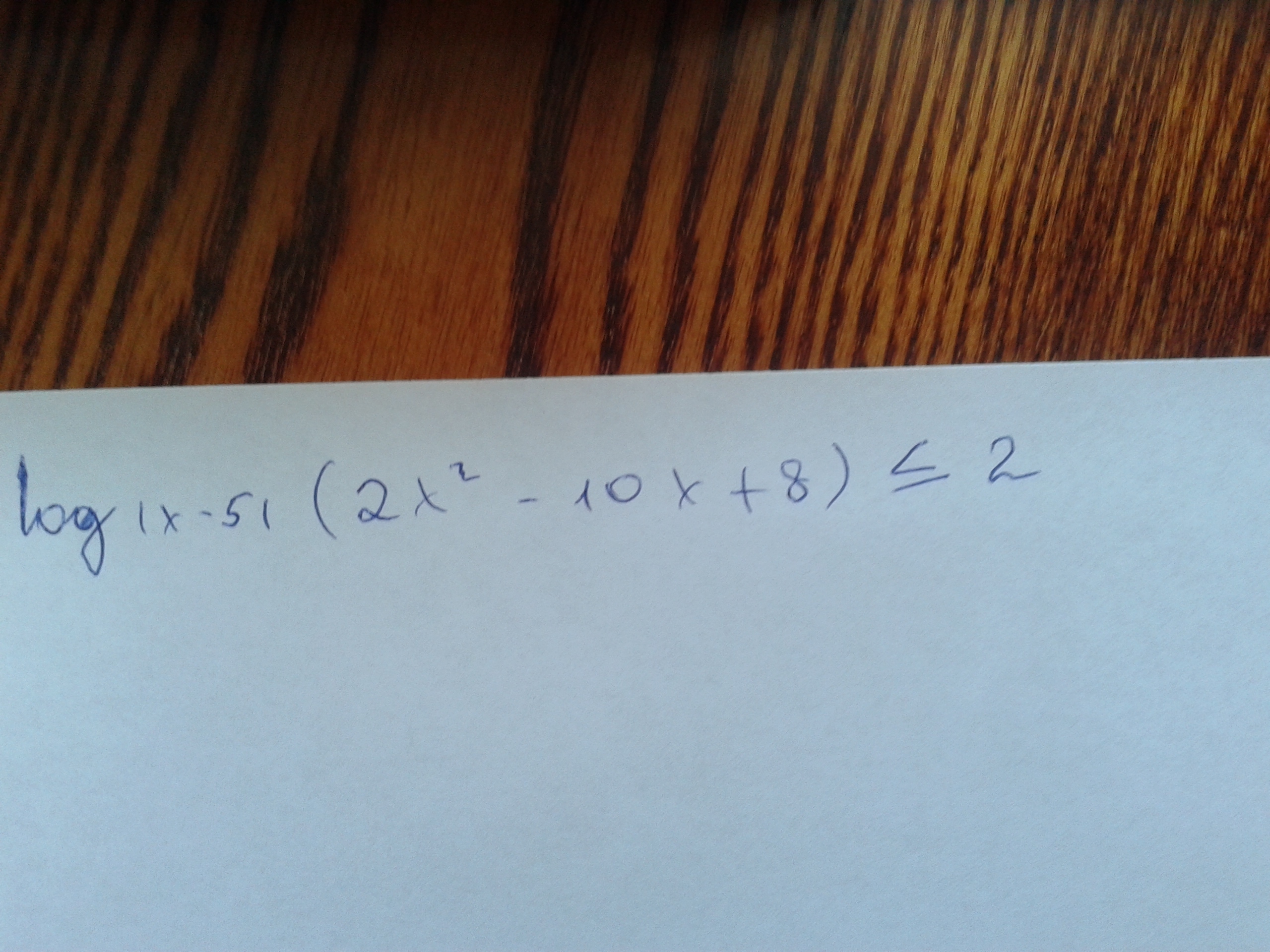
Ответы
Автор ответа:
0
Автор ответа:
0
Основание не =1
Похожие вопросы
Предмет: Русский язык,
автор: ayliniskenderova990
Предмет: Другие предметы,
автор: Nelgria
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: венялила