Question

Наити наибольшее и наименьшее значение функции f(x)=x^3+12x^2 +45x+20, на отрезке [-4;-2].плииз помогите!!

Answer 1

Найдем производную

F'=3x^2+24x+45

3x^2+24x+45=0

X^2+8x+15=0

(X+5)(x+3)=0

Вычислим значения в точке x=3 и на концах отрезка.

F(-4)=-64+192-180+20=-32

F(-3)=-27+108-135+20=-34

F(-2)=-8+48-90+20=-30

Наибольшее значение f(-2)=-30, наименьшее f(-3)=-34

Answer 2

$f(x)=x^{3}+12x^{2}+45x+20\f'(x)=3x^{2}+24x+45\3x^{2}+24x+45=0|:3\x^{2}+8x+15=0\D=64-60=4=2^{2};\x_{1}=frac{-8-2}{2}=-5;x_{2}=frac{-8+2}{2}=-3$

 

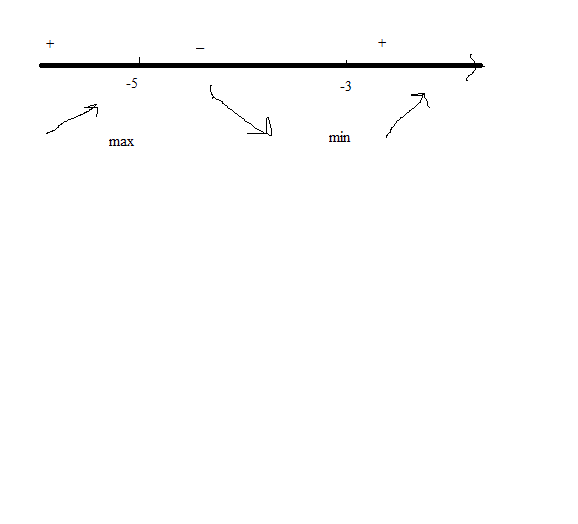
Найдем значение функциина концах отрезка и в точке минимума (см. вложение):

f(-4) = -64 +192 - 180 +20 = -32;

f(-3) = -27 + 108 - 135 +20 = -34;

f(-2) = -8 + 48 -90 +20 = -30.

Ответ: наибольшее значение функции f(x)=x^3+12x^2 +45x+20, на отрезке [-4;-2] есть -30, а наименьшее это -34.