Question

z=9x^2+4y^2-6x-4y+3

( Study the functions on extreme)
Изучите функцию на экстрем ( где макс где мин ) вроде как

Answer 1

$z(x,y)=9x^2+4y^2-6x-4y+3$
Находим подозрительные на экстремум точки. По необходимому условию экстремума, приравниваем первые частные производные нулю, решаем систему линейных алгебраических уравнений:
$left { {{ frac{dz}{dx}equiv18x-6=0, } atop { frac{dz}{dy}equiv8y-4=0, }} right.= textgreater left { {{x= frac{1}{3} } atop {y= frac{1}{2} }} right.$
Из достаточного условия экстремума следует, что если дифф. квадратичная форма положительна, то точка является точкой минимума, если отрицательна - максимума. Составим матрицу H из вторых частных производных заданной функции и вычислим её в стационарной точке (в данном случае элементы H - константы):
$H=left(begin{array}{cc} frac{partial^2z}{partial x^2} & frac{partial^2z}{partial xpartial y} \frac{partial^2z}{partial xpartial y} &frac{partial^2z}{partial y^2} \end{array}right)=left(begin{array}{cc} 18 & 0 \ 0 & 8 \end{array}right)$
Для определения знака квадратичной формы можно воспользоваться критерием Сильвестра: если все угловые миноры матрицы положительны, то квадратичная форма положительна, если у угловых миноров чередуется знак (причём первый отрицательный), то квадратичная форма отрицательна.
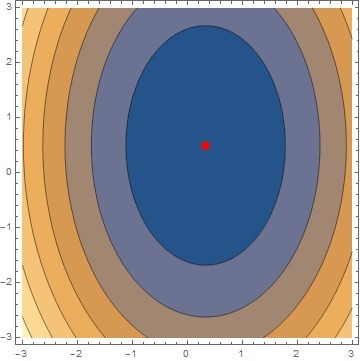
Первый элемент >0, определитель матрицы H >0, следовательно стационарная точка x=1/3, y=1/2 является локальным минимумом.
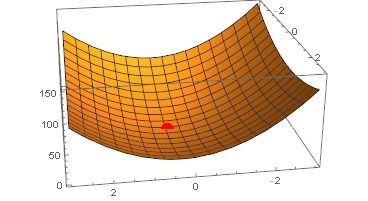
На изображениях представлены линии уровня и график заданной функции с точкой минимума.