Предмет: Алгебра,
автор: Arss13
341 (1), 343 (1) Заранее благодарю)
Приложения:

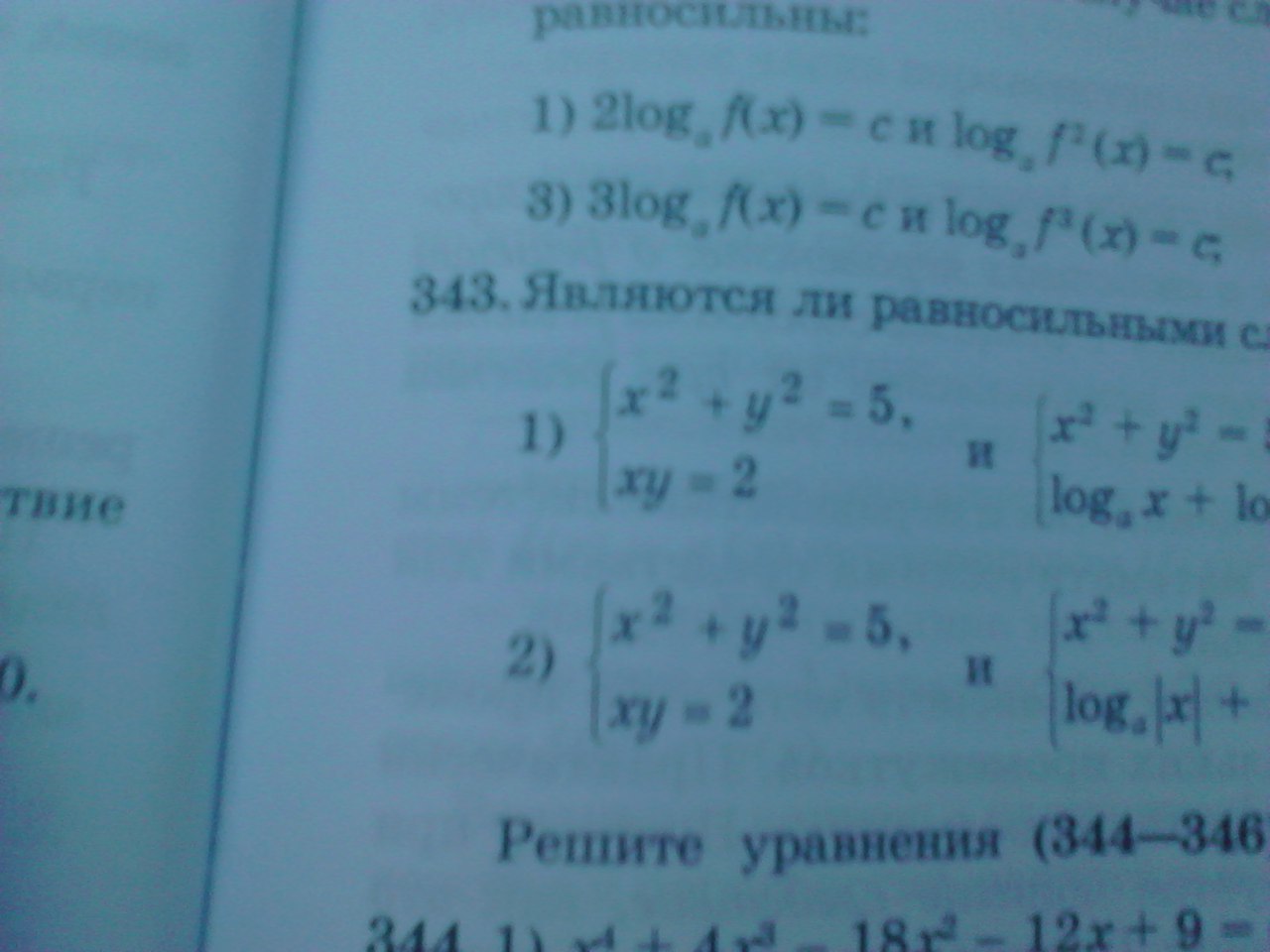
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: pr221916
Предмет: Биология,
автор: yulyaaaaa2007
Предмет: Математика,
автор: cemenguts051210
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: hatunya