Шар радиуса 3√2 касается всех ребер правильного тетраэдра.Определите длину ребер этого тетраэдра.
Ответы
Ну сначала надо это изобразить эту красоту. Очевидно, что шар описан около тетраэда.
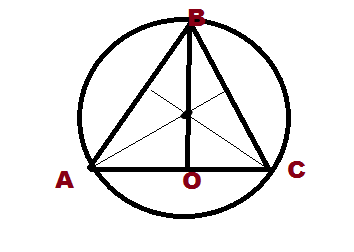
Второй чертеж - наша красота в сечении. То есть рассекаем через центр и вершину тетраэда. Получаем в сечении правильный треугольник, который вписан в круг. (я сделала его во вложении). Если мы построим медианы/высоты/биссекрисы, то они пересекуться в центре круга. По своействам правильного треугольника, его медианы/высоты/биссектрисы делятся точкой пересечения 2к1 от вершины то есть наш радиус это 2/3 от высоты треугольника. Находим высоту. (3√2*3)/2=4,5√2.
Теперь рассмотрим половину нашего треугольника, которую мы отделили высотой (то есть треугольник ОСВ. Угол С=60°, така как правильный треугольник.
sinC=BO/BC=√3/2
BO=4,5√2. BC - искомая сторона
4,5√2/BC=√3/2
4,5√2=√3/2 *ВС
9√2/√3 = ВС