Предмет: Геометрия,
автор: shiro5
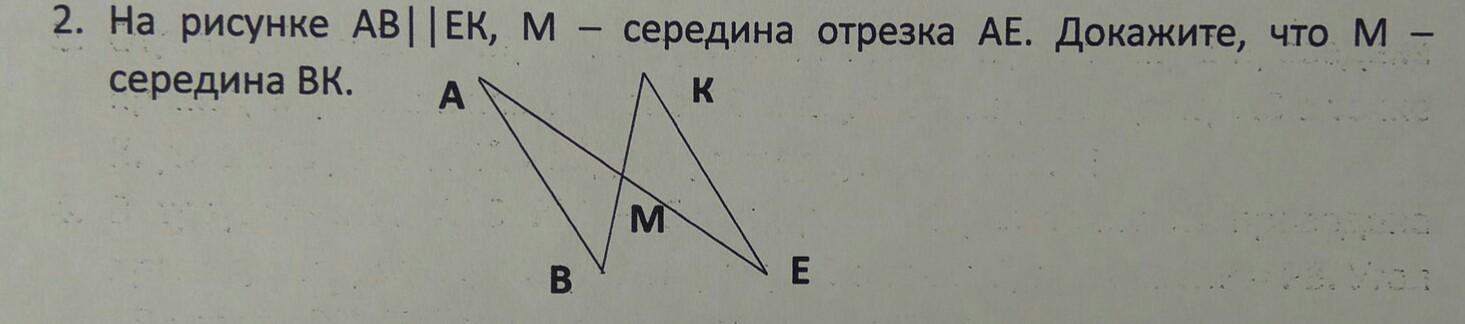
На рисунке AB||EK, M—середина отрезка AE.Докажите, что M—середина BK.
Приложения:
Ответы
Автор ответа:
0
Рассмотрим треугольники ACM и MDB и докажем что они равны:
1) AM=MB (так как М середина отрезка AB)
2) угол А= угол В (так как являются накрестлежащими углами при параллельных прямых AC и DB и секущей АВ)
3) угол AMC= угол DMB (так как вертикальные)
следовательно треугольник ACM = MDB
Раз треугольники равны значит CM=MD, если стороны равны, значит М середина
1) AM=MB (так как М середина отрезка AB)
2) угол А= угол В (так как являются накрестлежащими углами при параллельных прямых AC и DB и секущей АВ)
3) угол AMC= угол DMB (так как вертикальные)
следовательно треугольник ACM = MDB
Раз треугольники равны значит CM=MD, если стороны равны, значит М середина
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: galina220480
Предмет: Английский язык,
автор: vaa72
Предмет: Литература,
автор: Кирилл1111222233333