Предмет: Алгебра,
автор: Vladeee
найдите точку максимума функции. y=11+6sqrt(x)-2xsqrt(x)
Ответы
Автор ответа:
0
y'=
=
Приложения:

Автор ответа:
0
Находим производную.
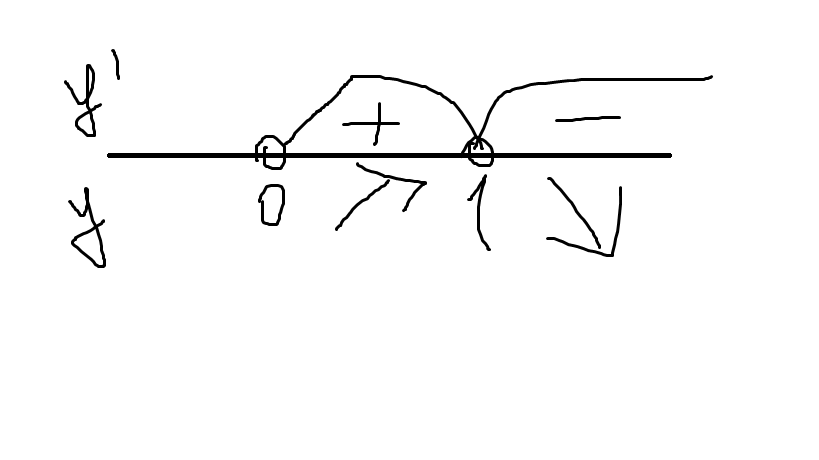
Найдём критические точки, приравняя производную к нулю. ОДЗ незабудем:
Вложение.
x=1 - точка максимума.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: anj22246
Предмет: Математика,
автор: Valeria345672
Предмет: Қазақ тiлi,
автор: zhanelzhumabai08
Предмет: Физика,
автор: airwaves
Предмет: Физика,
автор: Зинушка