Предмет: Алгебра,
автор: D1spatcher
Найти наименьшее и наибольшее значение функции
Приложения:
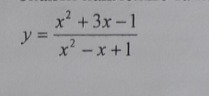
Ответы
Автор ответа:
0
Найдем производную и приравняем нулю:

Область определения разделена на 3 интервала:
1) (-беск; (1-корень(3)/2)
2) ((1-корень(3))/2; (1+корень(3))/2)
3) ((1+корень(3))/2; +беск)
Подставив значения из каждого интервала в производную определим знаки интервалов:
1) -
2) +
3) -
Так, как в точке (1-корень(3))/2 первая производная меняет знак с минуса на плюс, то это точка минимума. А в точке (1+корень(3))/2 производная меняет знак с плюса на минус, следовательно, точка максимума.

Область определения разделена на 3 интервала:
1) (-беск; (1-корень(3)/2)
2) ((1-корень(3))/2; (1+корень(3))/2)
3) ((1+корень(3))/2; +беск)
Подставив значения из каждого интервала в производную определим знаки интервалов:
1) -
2) +
3) -
Так, как в точке (1-корень(3))/2 первая производная меняет знак с минуса на плюс, то это точка минимума. А в точке (1+корень(3))/2 производная меняет знак с плюса на минус, следовательно, точка максимума.
Автор ответа:
0
Всем спасибо , особенно за ответ в письменном виде)
Автор ответа:
0
не люблю я с этим телефонном возится =) не за что)
Автор ответа:
0
Ответ на листочках.....................
Приложения:




Похожие вопросы
Предмет: Алгебра,
автор: profenovan
Предмет: Математика,
автор: aisaevaolha2088
Предмет: Алгебра,
автор: lll3568
Предмет: Алгебра,
автор: AnelyBer
Предмет: Информатика,
автор: Sokolkrominus