Предмет: Геометрия,
автор: bulka2020
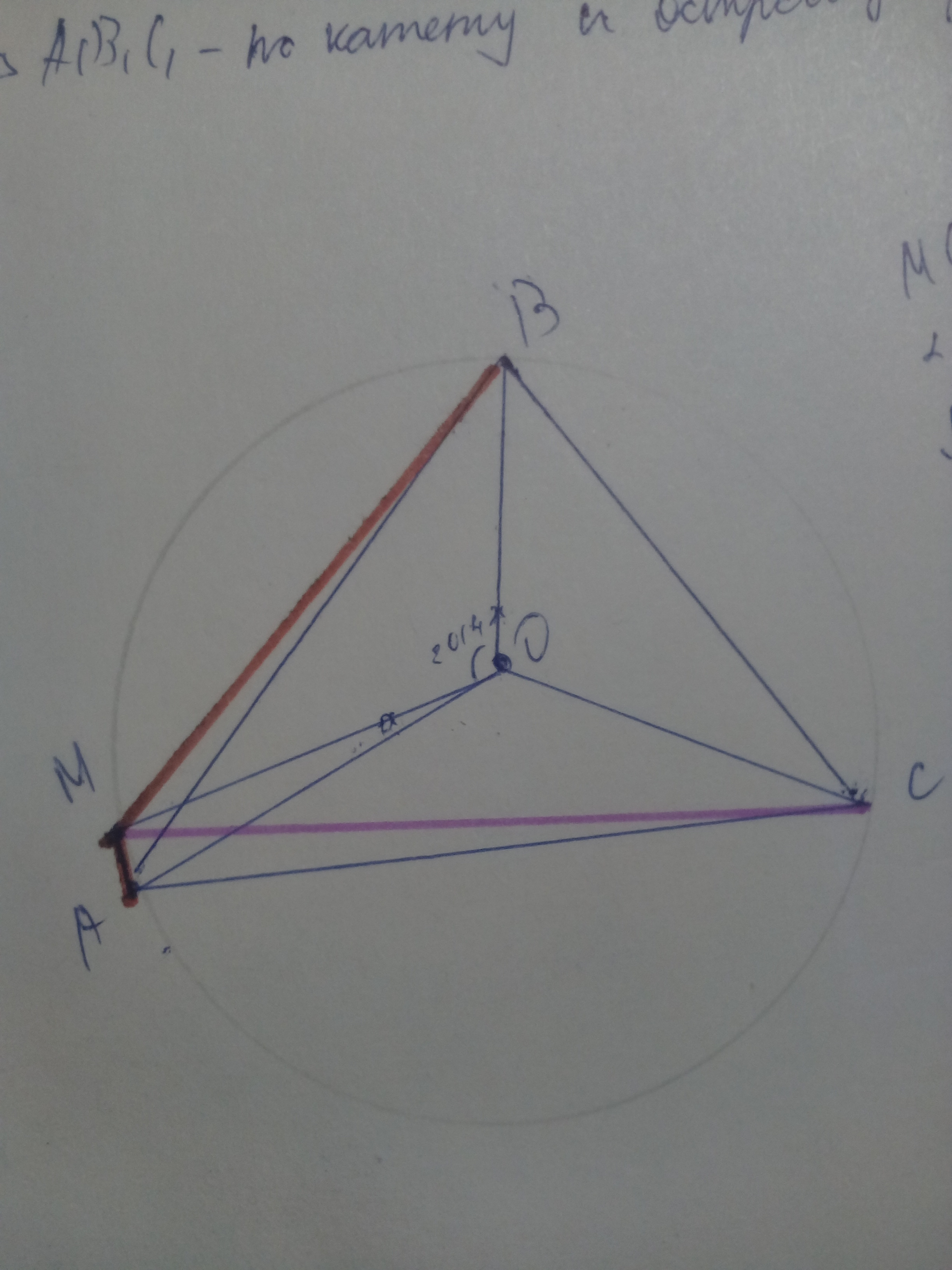
Пусть ABC — равносторонний треугольник, радиус описанной окружности которого равен 1, M — точка, которая делит дугу AC этой окружности в отношении 1:2014 считая от вершины A. Найдите MA^2+MB^2+MC^2.
Ответы
Автор ответа:
0
∠MOB = 360°/3 = 120°
∠AOM = 120°/(1 + 2014)° = (120/2015)° = (24/403)°
Т.е. ∠AOM → 0.
Раз ∠AOM → 0, то cosAOM → 1.
По теореме косинусов:
AM² → OM² + OA² - 2OM•OA•cosMAO
OM = OA = R
AM² → 2OM² - 2OM² (т.к. cosMAO → 1)
AM² → 0
AM → 0.
AC → MC и MB → AB, т.к. AM → 0, то MB и MC практически совпадают.
Т.к. w(O; R) - описанная, то AC = √3R = √3•1 = √3.
Тогда MB → √3 и MC → √3.
Тогда MB² + AM² + MC² = (√3)² + 0² + (√3)² = 3 + 3 = 6.
Ответ: 6.
∠AOM = 120°/(1 + 2014)° = (120/2015)° = (24/403)°
Т.е. ∠AOM → 0.
Раз ∠AOM → 0, то cosAOM → 1.
По теореме косинусов:
AM² → OM² + OA² - 2OM•OA•cosMAO
OM = OA = R
AM² → 2OM² - 2OM² (т.к. cosMAO → 1)
AM² → 0
AM → 0.
AC → MC и MB → AB, т.к. AM → 0, то MB и MC практически совпадают.
Т.к. w(O; R) - описанная, то AC = √3R = √3•1 = √3.
Тогда MB → √3 и MC → √3.
Тогда MB² + AM² + MC² = (√3)² + 0² + (√3)² = 3 + 3 = 6.
Ответ: 6.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Ebantireks
Предмет: Английский язык,
автор: tukenElnur
Предмет: Русский язык,
автор: almyrza2007
Предмет: Математика,
автор: котя35