Предмет: Геометрия,
автор: TanyWM
в треугольнике АВС, АС=4, соsА=-0.8, соsС=8/ на корень из 73. Найдите площадь треугольника АВС. Помогите пожалуйста
Ответы
Автор ответа:
0
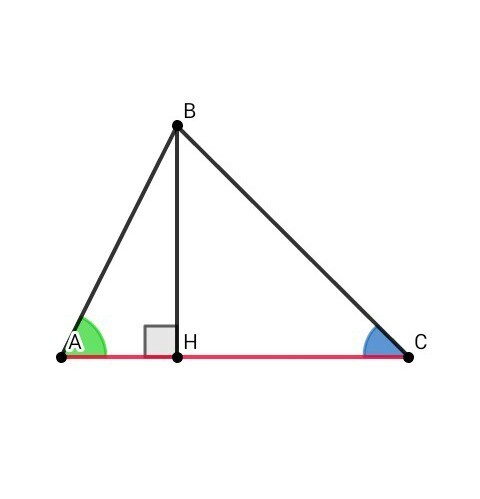
1) Рассмотрим рис. 2
Опустим высоту ВН на АС:
Пусть АН = х, СН = у, ВН = h, тогда
Рассмотрим ∆ АНВ:
ctgA = х/h → x = h·ctgA
Рассмотрим ∆ СНВ:
ctgC = y/h → y = h·ctgC
AC = x + y = h·ctgA + h·ctgC = h·( ctgA + ctgC ) →
h = AC/( ctgA + ctgC )
Площадь треугольника вычисляется по формуле через известную сторону и высоту, проведённую к этой стороне.
S abc = ( 1/2 )·AC·h = ( 1/2 )·АС·( AC/( ctgA + ctgC ) ) = ( 1/2 )· ( AC²/( ctgA + ctgC ) )
Значит, площадь треугольника вычисляется через известную сторону и известные котангенсы прилежащих углов.
__________________
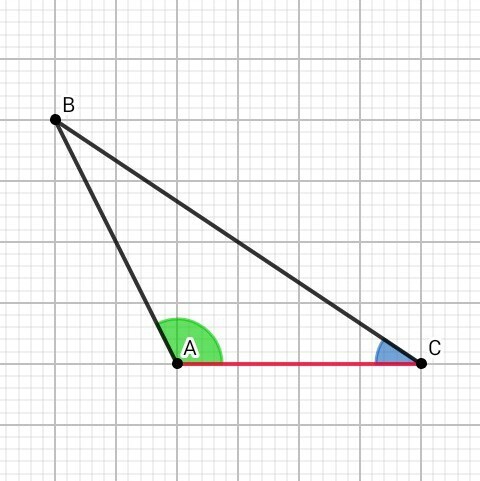
2) Рассматриваем рис. 1 :
По условии косинус угла А отрицательный, значит угол А тупой →
∆ АВС – тупоугольный.
Используем формулу площади треугольника для решения данной задачи:
S abc = ( 1/2 )·( AC²/( ctgA + ctgС ) )
__________________________
ctga = cosa/sina
Возведём обе части в квадрат, с учетом, что sin²a = 1 – cos²a →
ctg²а = cos²a/sin²a = cos²a/( 1 – cos²a )
ctga = ± √( cos²a/( 1 – cos²a ) )
Перейдём к нашему случаю, котангенс тупого угла отрицательный →
ctgA = – √( ( - 0,8 )²/( 1 - ( - 0,8 )² ) ) = – √( 0,64 / 0,36 ) = – √( 64/36 ) = – 8/6 = – 4/3
ctgС = + √( ( 8/√73 )²/( 1 - ( 8/√73 )² ) ) = √( ( 64/73 )/( 9/73 ) ) = √( 64/9 ) = 8/3
__________________________
S abc = ( 1/2 )·( AC²/( ctgA + ctgС ) ) = ( 1/2 )·( 4² / ( – 4/3 + 8/3 ) ) = ( 1/2 )·( 16/( 4/3 ) ) = ( 1/2 ) · 12 = 6
ОТВЕТ: S abc = 6
Опустим высоту ВН на АС:
Пусть АН = х, СН = у, ВН = h, тогда
Рассмотрим ∆ АНВ:
ctgA = х/h → x = h·ctgA
Рассмотрим ∆ СНВ:
ctgC = y/h → y = h·ctgC
AC = x + y = h·ctgA + h·ctgC = h·( ctgA + ctgC ) →
h = AC/( ctgA + ctgC )
Площадь треугольника вычисляется по формуле через известную сторону и высоту, проведённую к этой стороне.
S abc = ( 1/2 )·AC·h = ( 1/2 )·АС·( AC/( ctgA + ctgC ) ) = ( 1/2 )· ( AC²/( ctgA + ctgC ) )
Значит, площадь треугольника вычисляется через известную сторону и известные котангенсы прилежащих углов.
__________________
2) Рассматриваем рис. 1 :
По условии косинус угла А отрицательный, значит угол А тупой →
∆ АВС – тупоугольный.
Используем формулу площади треугольника для решения данной задачи:
S abc = ( 1/2 )·( AC²/( ctgA + ctgС ) )
__________________________
ctga = cosa/sina
Возведём обе части в квадрат, с учетом, что sin²a = 1 – cos²a →
ctg²а = cos²a/sin²a = cos²a/( 1 – cos²a )
ctga = ± √( cos²a/( 1 – cos²a ) )
Перейдём к нашему случаю, котангенс тупого угла отрицательный →
ctgA = – √( ( - 0,8 )²/( 1 - ( - 0,8 )² ) ) = – √( 0,64 / 0,36 ) = – √( 64/36 ) = – 8/6 = – 4/3
ctgС = + √( ( 8/√73 )²/( 1 - ( 8/√73 )² ) ) = √( ( 64/73 )/( 9/73 ) ) = √( 64/9 ) = 8/3
__________________________
S abc = ( 1/2 )·( AC²/( ctgA + ctgС ) ) = ( 1/2 )·( 4² / ( – 4/3 + 8/3 ) ) = ( 1/2 )·( 16/( 4/3 ) ) = ( 1/2 ) · 12 = 6
ОТВЕТ: S abc = 6
Приложения:
Похожие вопросы