Question

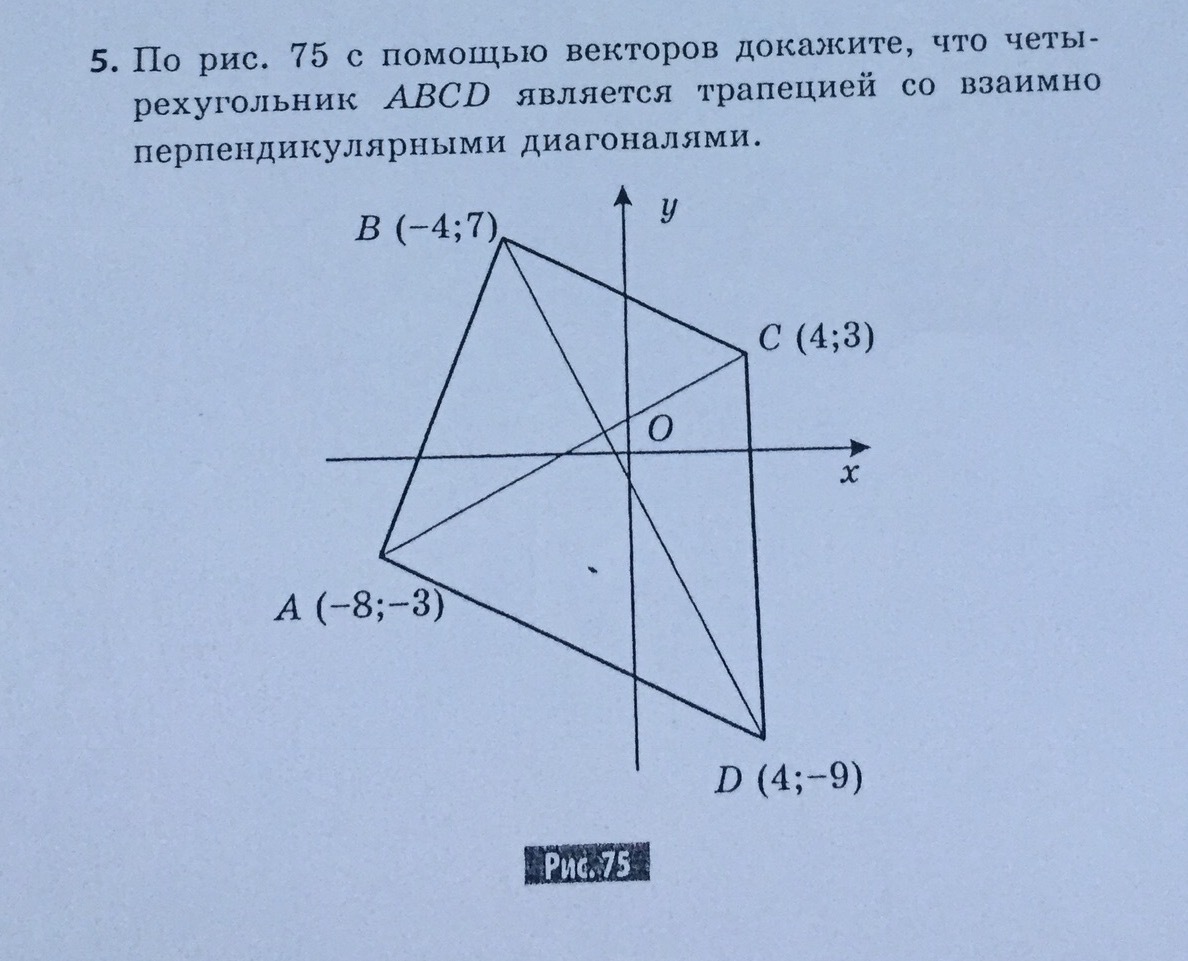
По рисунку с помощью векторов докажите, что четырёхугольник ABCD является трапецией со взаимно перпендикулярными диагоналями.

Answer 1

$bar{AD}{4-(-8);-9-(-3)}={12;-6};$
$bar{BC}{4-(-4);3-7}={8;-4}; bar{BC}=frac{2}{3}bar{AB}Rightarrow$

AD параллельно BC.

$bar{AC}{4-(-8);3-(-3)}={12; 6};$
$bar{BD}{4-(-4);-9-7}={8;-16}.$

Скалярное произведение $(bar{AC};bar{BD})=12cdot 8+6cdot (-16)=96-96=0Rightarrow bar{AC}perp bar{BD}$

Замечание. Перед взятием скалярного произведения можно было заменить векторы на векторы того же направления, но меньшей длины. Скажем, первый вектор естественно поделить на 6, а второй на 8.