Предмет: Алгебра,
автор: kristinavodyanaya
ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА. ЗАВТРА НАДО ПЕРЕСДАВАТЬ ЖТО А Я ВООбЩЕ НЕ ЗНАЮ. Алгебра лабораторная работа вариант 1. Помогите 11 класс
Приложения:

Ответы
Автор ответа:
0
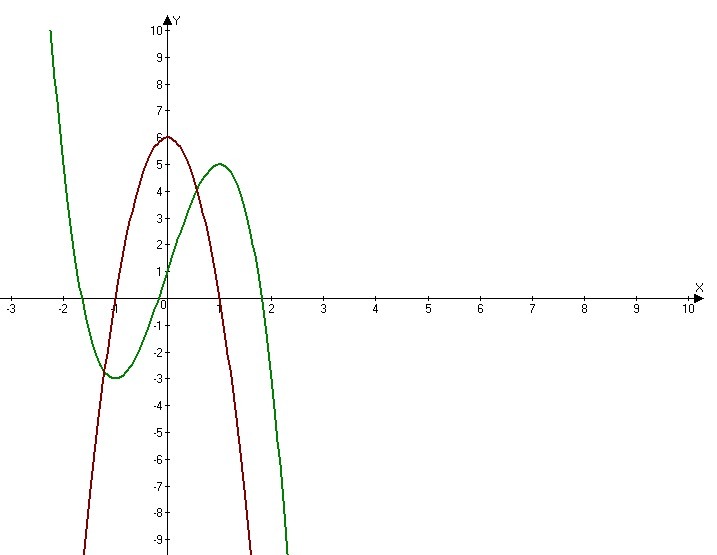
Задание 1.
1) Область определения функции: множество всех действительных чисел или
2) Производная функции:
3) Критические точки
Приравниваем производную функции к нулю:
4) Промежутки монотонности и экстремумы. По результатам исследования составьте таблицу
В окрестности точки x = -1 производная функции меняет знак с (-) на (+). Следовательно, точка x = -1 - точка минимума. В окрестности точки x = 1 производная функции меняет знак с (+) на (-). Следовательно, точка x = 1 - точка максимума.
Таблицу смотреть во вложении.
y=6x-2x^3+1 строим по точкам (2;-3), (-2;5), (-1; -3), (1; 5), (0;1)..
y = 6 - 6x^2 - парабола, ветви направлены вниз
3) Уравнение касательной в точке х0=2 и угол наклона?
Уравнение касательной имеем вид:
Вычислим значение функции в точке х0
Вычислим значение производной в точке х0
Уравнение касательной:
Геометрический смысл производной заключается в том, что производная равна угловому коэффициенту касательной и тангенсу угла наклона, то есть:
Приложения:

Похожие вопросы
Предмет: Физика,
автор: noname1863
Предмет: Английский язык,
автор: rosha22021983
Предмет: Математика,
автор: emilka43
Предмет: Биология,
автор: Лейна1