Предмет: Алгебра,
автор: Lizaveta20000817
Помогите решить 1 номер, пожалуйста!!((
Приложения:

Ответы
Автор ответа:
0
Автор ответа:
0
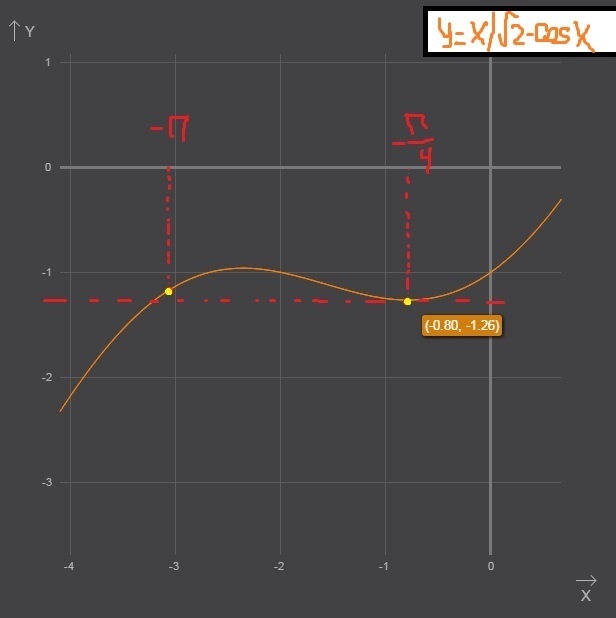
Я посчитала приблизительные значения для того чтоб можно было сравнить ответы и найти наибольшее и наименьшее значения)
Наименьшим оказалось примерно -1,2.
Но в ответе мы запишем как (наим.) =
(наим.) = 
Наибольшее значение - примерно 3,1. В ответ пойдет (наиб.) =
(наиб.) = 
Наименьшим оказалось примерно -1,2.
Но в ответе мы запишем как
Наибольшее значение - примерно 3,1. В ответ пойдет
Приложения:

Автор ответа:
0
и правда)
Автор ответа:
0
я уже сам пересчитал
Автор ответа:
0
это не мешает взглянуть на график :)
Похожие вопросы
Предмет: Русский язык,
автор: mortis2799
Предмет: Физика,
автор: mailwtf2
Предмет: Физика,
автор: nurayhasanova
Предмет: Биология,
автор: Akhmadova71
Предмет: Химия,
автор: AvErLiN