Предмет: Алгебра,
автор: Кариночка78
Помогите решить уравнение. Подробно.
Приложения:

Ответы
Автор ответа:
0
Надеюсь, достаточно подробно. Все решается по формуле, которую я написала вверху, а также методом замены. Дальше решаются квадратные уравнения.
Прости за грязь.
Прости за грязь.
Приложения:
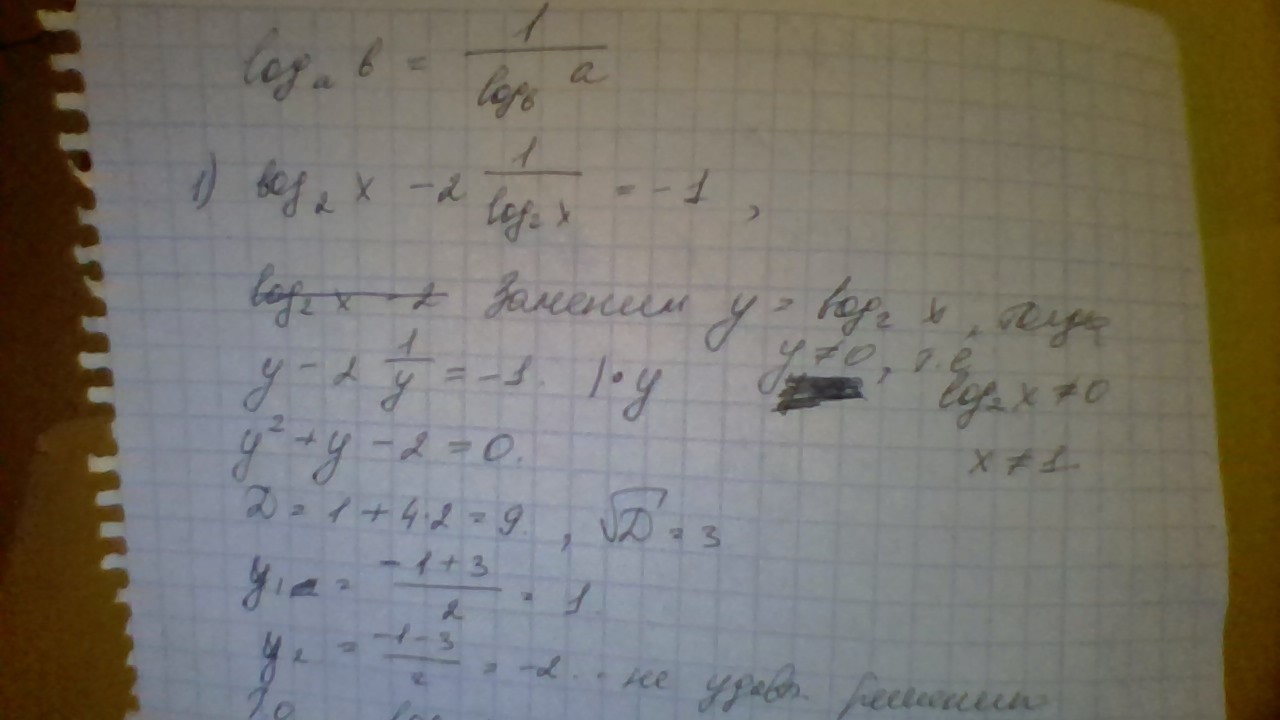

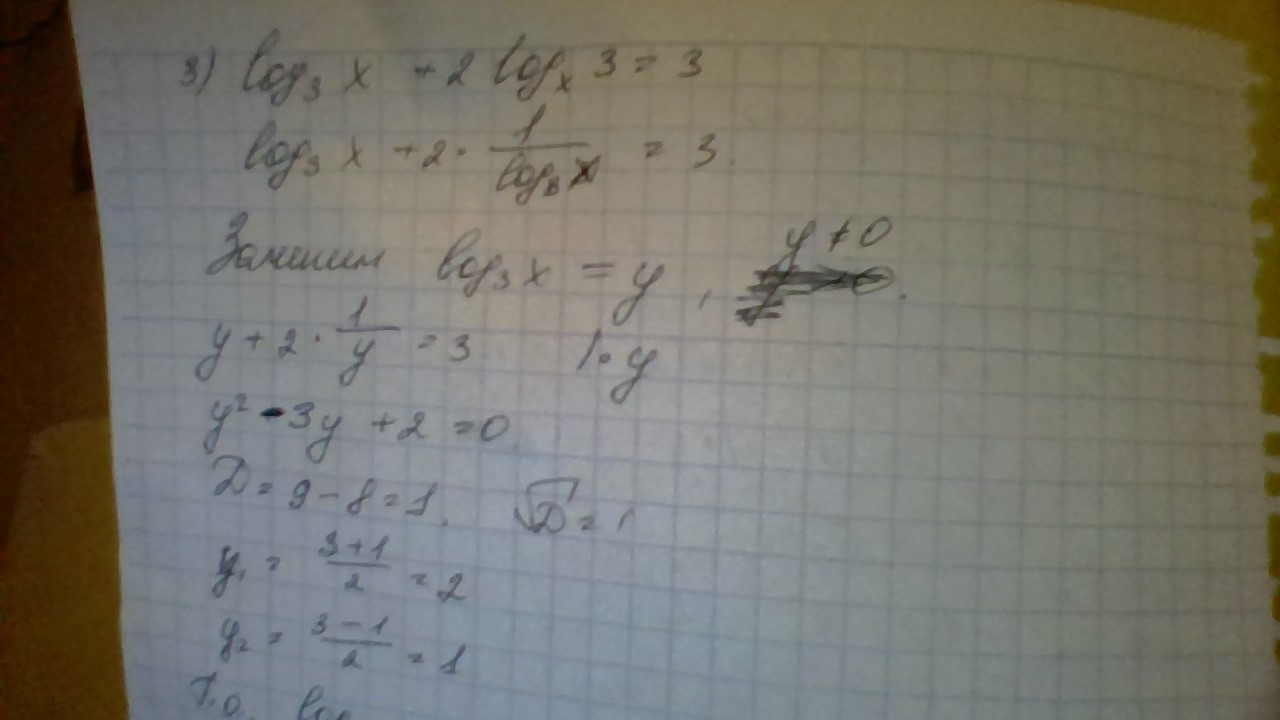

Автор ответа:
0
Приложения:
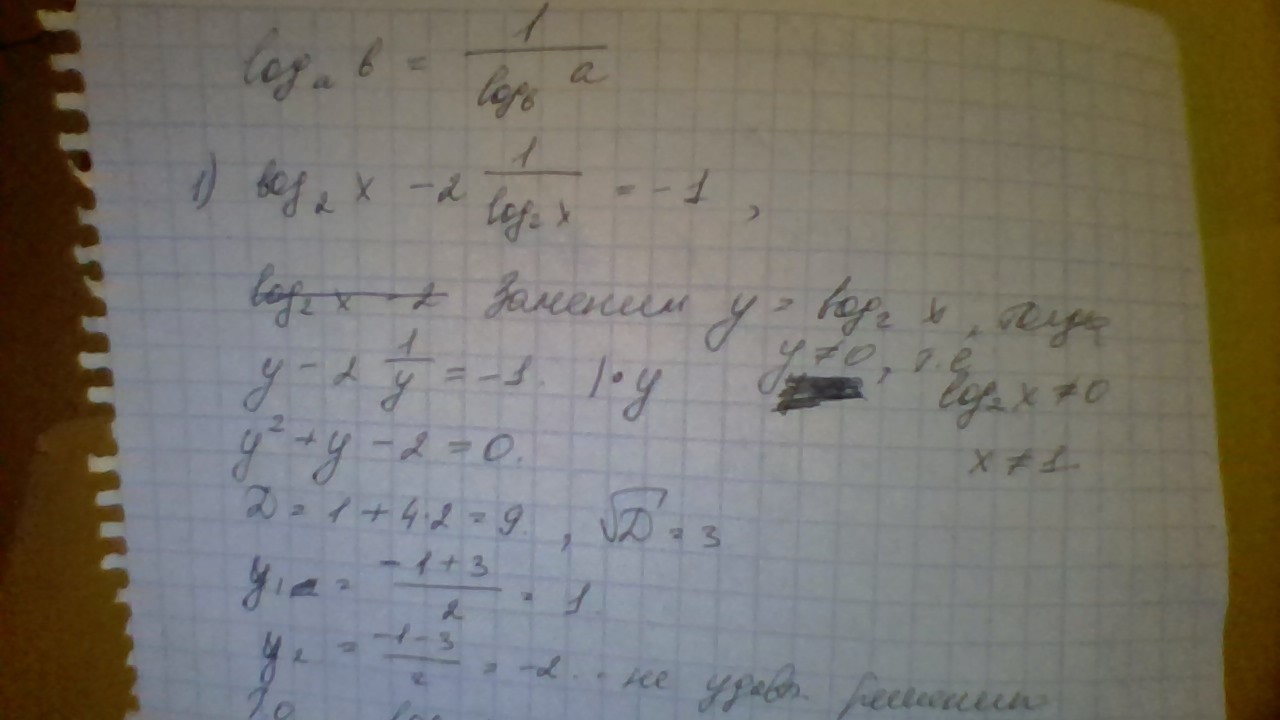

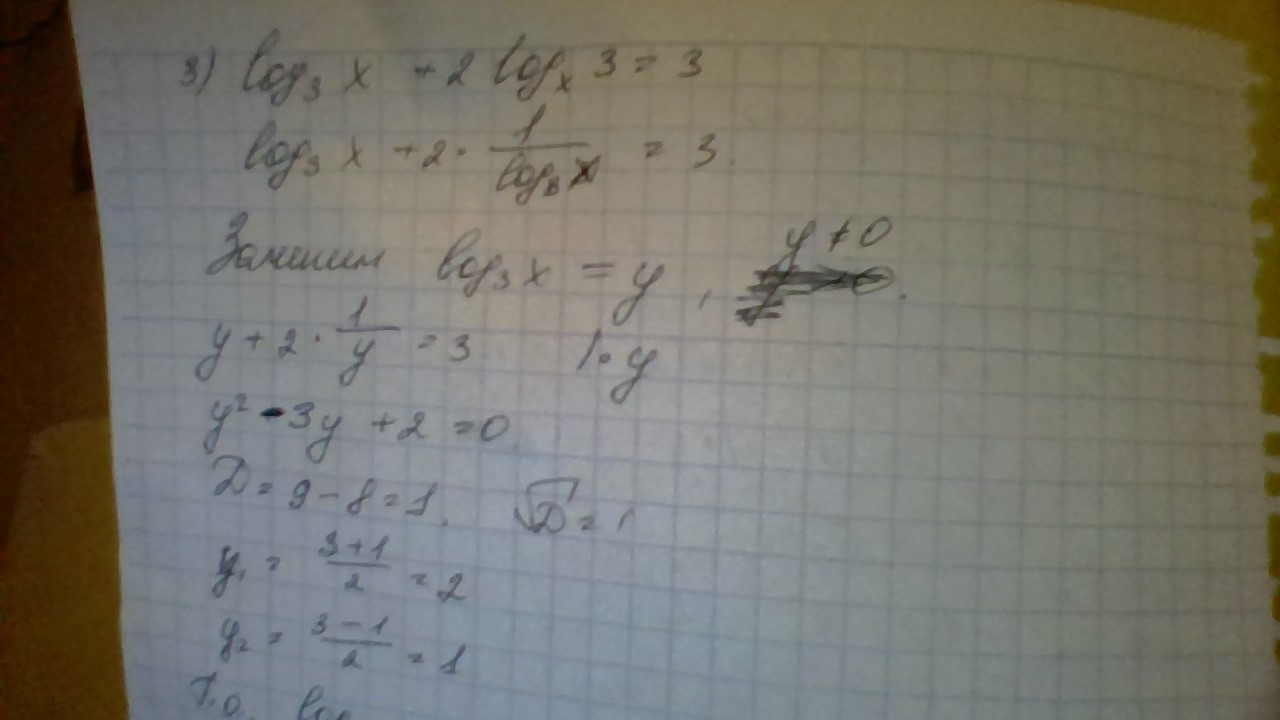

Похожие вопросы
Предмет: Английский язык,
автор: maksimnikolai123
Предмет: Английский язык,
автор: maksimnikolai123
Предмет: Математика,
автор: nikolaevaalisa65
Предмет: Право,
автор: sergejjkirjashk
Предмет: География,
автор: Камиля1333