Предмет: Математика,
автор: mefody66
Очередная 26 задача из ОГЭ.
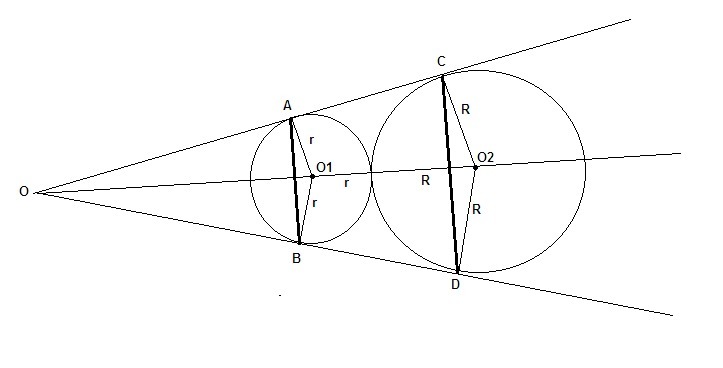
Две окружности, вписанные в угол О, касаются друг друга внешним образом.
Точки A, B, C, D - точки касания окружностей и угла.
O1 и O2 - центры окружностей.
Их радиусы r = 15, R = 21.
Рисунок прилагается.
Требуется:
1) Определить, параллельны ли отрезки AB и CD.
(Мне кажется - не всегда!)
2) Найти наименьшее расстояние между этими отрезками.
Если они параллельны, то просто найти расстояние между ними.
В учебнике ответ 35, но мне кажется, что это опечатка и должно быть 15+21=36.
Как это решить?
Приложения:
Ответы
Автор ответа:
0
отрезки AB и CD параллельны всегда - можно доказывать, рассматривая равенства всяких треугольников, но проще заметить, что имеется симметрия относительно биссектрисы угла О - если бы отрезки были не параллельны - не было бы симметрии.
обозначим MN - расстояние между AB и CD
далее проще использовать тригонометрию
обозначим половину угла О через







Ответ: 35
обозначим MN - расстояние между AB и CD
далее проще использовать тригонометрию
обозначим половину угла О через
Ответ: 35
Автор ответа:
0
это стандартная формула и свойство - угол О зависит только от R и r
Автор ответа:
0
Извините, я ничего не понял. Откуда вы взяли, что O2K = R-r и что угол O2O1K = a = половине угла О?
Похожие вопросы
Предмет: Математика,
автор: dnmdnm002
Предмет: Другие предметы,
автор: davydovmatvey84
Предмет: Математика,
автор: milanagab1507
Предмет: Литература,
автор: dinusja14