Question

С4! ВНИМАНИЕ! КТО НЕ ЗНАЕТ КАК ДЕЛАТЬ НЕ ДЕЛАЙТЕ! Кто будет писать бред ради пунктов - жалоба.

Нужны 2 случая! +чертежи.

Две стороны треугольника равны 4 и 10, косинус угла между ними равен 1/5. В треугольник вписан ромб, имеющий с треугольниками общий угол (вершина ромба, противоположная вершине этого угла, лежит на третьей стороне треугольника.) Найдите сторону ромба.

Answer 1

См.рис. во вложении и расчет тоже там же.. кажется там все должно быть понятно.

 

Answer 2

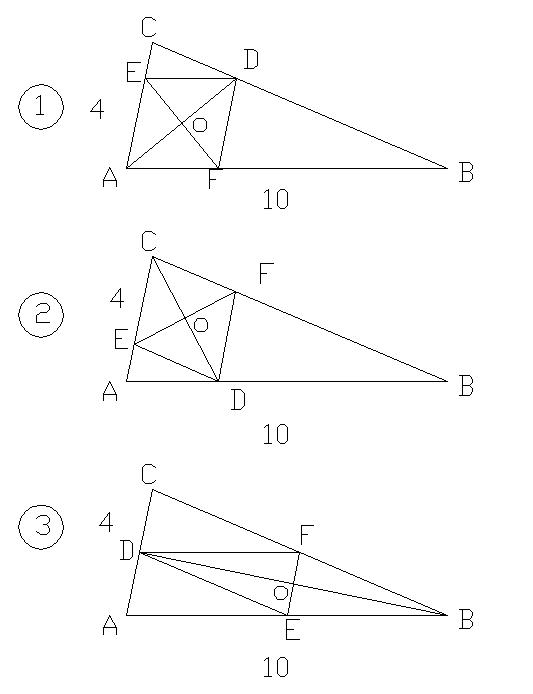
Пусть дано:

AC=4; BC=10; cos<ACB=1/5=0,2; DEFC - ромб

Найти: EF - ?

Решение:

Найдем сторону AB по теореме косинусов:

 

$AB^2=AC^2+BC^2-2AC cdot BCcosACB \ \ AB^2=16+100-2*4*10*0,2 \ \ AB^2=100 \ \ AB=10$

 

CE - биссектриса (как диагональ ромба, которая делит <C пополам) поэтому

AE:EB=4:10

AE:EB=2:5

Пусть AE=2x и EB=5x

AE+EB=AB

2x+5x=10

7x=10

x=10/7

EB=5x=5*10/7=50/7

Треугольники ABC и EBF - подобны (AC II EF, значит <ACB=<EFB и <B - общий)

Коэффициент подобия равен:

k=AB:EB=10:(50/7)=10*7/50=7/5

AC:EF=k=7/5

4/EF=7/5

EF=4*5/7=20/7

Ответ: 20/7