Предмет: Алгебра,
автор: Viktor121234
помогите решить логарифмы
1 уравнение
2 неравенства
Приложения:
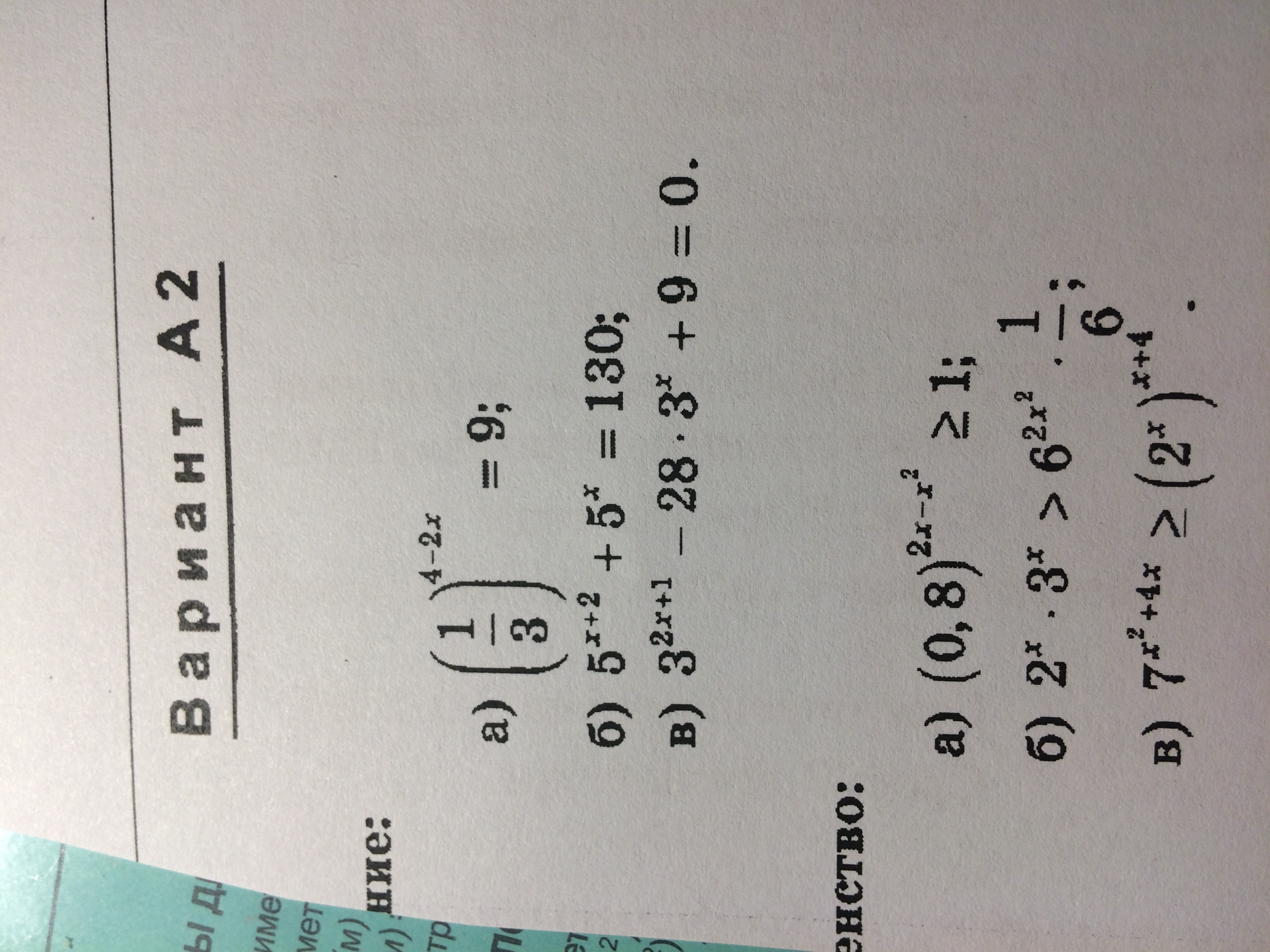
Ответы
Автор ответа:
0
Уравнения:

Неравенства:
![displaystyle 0,8^{2x-x^2} geq 1\\(frac{4}{5})^{2x-x^2} geq (frac{4}{5})^0\\2x-x^2 leq 0;big|;*(-1)\x(x-2) geq 0\\x_1=0; qquad x_2=2;\\+++0---2+++\\xin(-ifty;0] cup [2; +infty);\\\2^xcdot3^x textgreater 6^{2x^2}cdot frac{1}{6}\6^x textgreater 6^{-1}cdot 6^{2x^2}\6^x textgreater 6^{2x^2-1}\x textgreater 2x^2-1\2x^2-x-1 textless 0\D:1+8=9=3^2\\x_1,_2=frac{1pm3}{4}; qquad x_1=1, qquad x_2=-frac{1}{2};\\+++(-frac{1}{2})---1+++ \\xin (-frac{1}{2};1); displaystyle 0,8^{2x-x^2} geq 1\\(frac{4}{5})^{2x-x^2} geq (frac{4}{5})^0\\2x-x^2 leq 0;big|;*(-1)\x(x-2) geq 0\\x_1=0; qquad x_2=2;\\+++0---2+++\\xin(-ifty;0] cup [2; +infty);\\\2^xcdot3^x textgreater 6^{2x^2}cdot frac{1}{6}\6^x textgreater 6^{-1}cdot 6^{2x^2}\6^x textgreater 6^{2x^2-1}\x textgreater 2x^2-1\2x^2-x-1 textless 0\D:1+8=9=3^2\\x_1,_2=frac{1pm3}{4}; qquad x_1=1, qquad x_2=-frac{1}{2};\\+++(-frac{1}{2})---1+++ \\xin (-frac{1}{2};1);](https://tex.z-dn.net/?f=displaystyle+0%2C8%5E%7B2x-x%5E2%7D+geq+1%5C%5C%28frac%7B4%7D%7B5%7D%29%5E%7B2x-x%5E2%7D+geq+%28frac%7B4%7D%7B5%7D%29%5E0%5C%5C2x-x%5E2++leq++0%3Bbig%7C%3B%2A%28-1%29%5Cx%28x-2%29++geq++0%5C%5Cx_1%3D0%3B+qquad+x_2%3D2%3B%5C%5C%2B%2B%2B0---2%2B%2B%2B%5C%5Cxin%28-ifty%3B0%5D+cup+%5B2%3B+%2Binfty%29%3B%5C%5C%5C2%5Excdot3%5Ex+textgreater++6%5E%7B2x%5E2%7Dcdot+frac%7B1%7D%7B6%7D%5C6%5Ex+textgreater++6%5E%7B-1%7Dcdot+6%5E%7B2x%5E2%7D%5C6%5Ex+textgreater++6%5E%7B2x%5E2-1%7D%5Cx+textgreater++2x%5E2-1%5C2x%5E2-x-1+textless++0%5CD%3A1%2B8%3D9%3D3%5E2%5C%5Cx_1%2C_2%3Dfrac%7B1pm3%7D%7B4%7D%3B+qquad+x_1%3D1%2C+qquad+x_2%3D-frac%7B1%7D%7B2%7D%3B%5C%5C%2B%2B%2B%28-frac%7B1%7D%7B2%7D%29---1%2B%2B%2B+%5C%5Cxin+%28-frac%7B1%7D%7B2%7D%3B1%29%3B)

Неравенства:
Похожие вопросы
Предмет: Алгебра,
автор: varyapanshyna78
Предмет: Английский язык,
автор: wasska79
Предмет: Геометрия,
автор: OlgaKovaleova
Предмет: Обществознание,
автор: elmira992