Предмет: Алгебра,
автор: ponvladis452
На отрезке AB выбрана точка C так, что AC=68 и BC=17 . Построена окружность с центром A , проходящая через C . Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
срочно решите пожалуйста.
Ответы
Автор ответа:
0
Ответ:
ВМ=51
Объяснение:
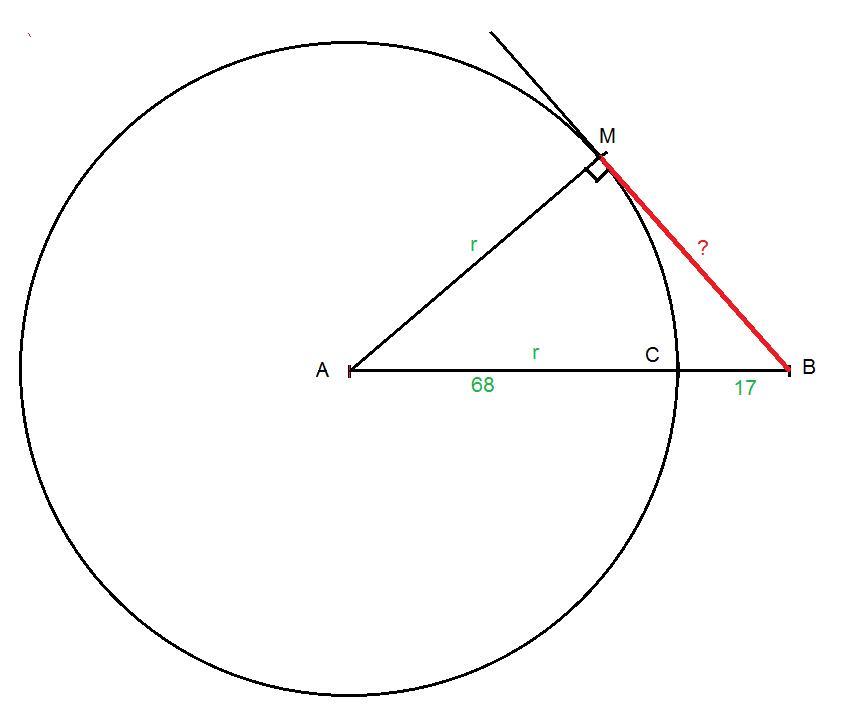
Дано: АВ - отрезок; С∈АВ; АС=68; СВ=17; А - центр окружности с радиусом АС; ВМ - касательная к окружности.
Найти: ВМ.
Решение:
Проведем отрезок АМ. АМ - радиус окружности, проведенный в точку касания прямой ВМ и окружности. Значит АМ⊥ВМ, и ΔАМВ прямоугольный.
АМ=АС=r=68.
АВ=АС+СВ=68+17=85.
По теореме Пифагора найдем катет ВМ.
Ответ: ВМ=51.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: irabahova2
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: fatimanisanbaeva2
Предмет: Алгебра,
автор: leratsvetkova3