Предмет: Геометрия,
автор: Ferler
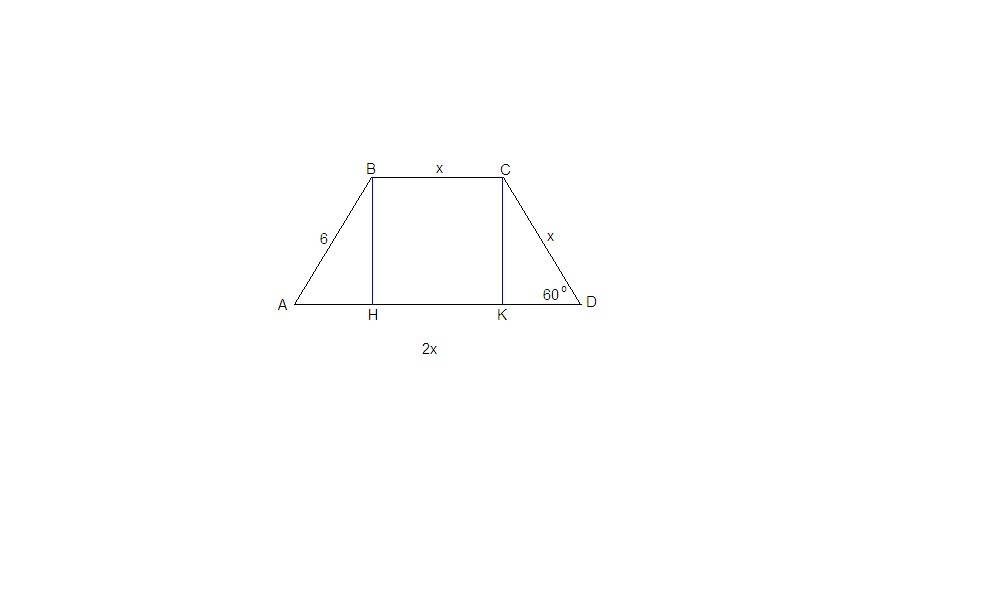
В трапеции АВСД основание АД вдвое больше основания ВС и вдвое больше боковой стороны СД. Угол АДС равен 60*, сторона АВ равна 6. Найдите площадь трапеции.
Ответы
Автор ответа:
0
Проведем высоты ВН и СК.
ВНКС - прямоугольник (ВН = СК как высоты трапеции, ВН║СК как перпендикуляры к одной прямой), значит
КН = ВС = х
Из прямоугольного треугольника CKD:
KD = CD · cos60° = x ·1/2 = x/2
AH = AD - KH - KD = 2x - x - x/2 = x/2, значит
ΔABH = ΔDCK по двум катетам, ⇒
CD = AB = 6.
AD = 2CD = 12.
Из ΔDCK:
СК = CD · sin60° = 6 · √3/2 = 3√3
Sabcd = (AD + BC)/2 · CK = (12 + 6)/2 · 3√3 = 27√3
ВНКС - прямоугольник (ВН = СК как высоты трапеции, ВН║СК как перпендикуляры к одной прямой), значит
КН = ВС = х
Из прямоугольного треугольника CKD:
KD = CD · cos60° = x ·1/2 = x/2
AH = AD - KH - KD = 2x - x - x/2 = x/2, значит
ΔABH = ΔDCK по двум катетам, ⇒
CD = AB = 6.
AD = 2CD = 12.
Из ΔDCK:
СК = CD · sin60° = 6 · √3/2 = 3√3
Sabcd = (AD + BC)/2 · CK = (12 + 6)/2 · 3√3 = 27√3
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: aishapwl
Предмет: Математика,
автор: borkivskao
Предмет: Русский язык,
автор: korkemabd
Предмет: Алгебра,
автор: toshiro97