Предмет: Математика,
автор: Mark090886
Тангенс острого угла прямоугольной трапеции равен 9 пятых Найдите ее большее основание если меньшее основание равно высоте и равно 54
Ответы
Автор ответа:
0
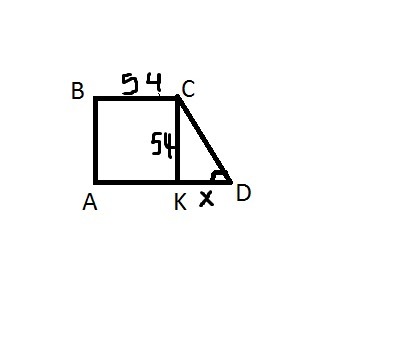
Пусть ABCD прямоугольная трапеция.
BC=CK (по условию)⇒CK=54
BC и AD- основания трапеции
Пусть высота CK⊥AD,тогда CK делит отрезок AD на отрезки AK и KD
AD=AK+KD
Так как BC║AK и BA║CK то ACKB- параллелограмм⇒ BC =AK,BA=CK⇒
AK=54 ⇒ AD=54+ KD
Так как CK⊥AD,то ΔCKD прямоугольный
tg D=9/5
tg D=54/x
Составим пропорцию
9/5=54/x
9x=54*5
x=(54*5)/9=6*5=30
BC=CK (по условию)⇒CK=54
BC и AD- основания трапеции
Пусть высота CK⊥AD,тогда CK делит отрезок AD на отрезки AK и KD
AD=AK+KD
Так как BC║AK и BA║CK то ACKB- параллелограмм⇒ BC =AK,BA=CK⇒
AK=54 ⇒ AD=54+ KD
Так как CK⊥AD,то ΔCKD прямоугольный
tg D=9/5
tg D=54/x
Составим пропорцию
9/5=54/x
9x=54*5
x=(54*5)/9=6*5=30
Приложения:
Похожие вопросы
Предмет: Литература,
автор: lolka23499
Предмет: Английский язык,
автор: filippovfilipp327
Предмет: История,
автор: karnauhovdaniil55
Предмет: Литература,
автор: KaterGood