Предмет: Алгебра,
автор: kapraldan
а)Решите уравнение.
б)Найдите миним расстояние и миним длину дуги между несовпадающими точками еденичн окружности,соответствующими корням уравнения.
Приложения:
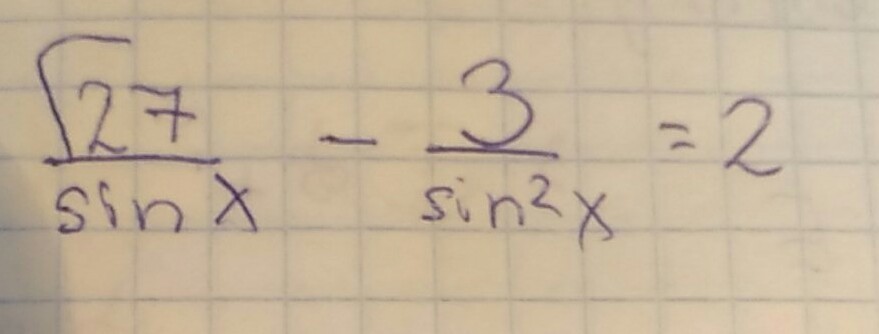
Ответы
Автор ответа:
0
Таким образом, sin(x) = √3 или sin(x) = √3/2. Заметим, что первое уравнение решений не имеет по определению синуса. Тогда решим уравнение sin(x) = √3/2, которое является частным случаем: x = π/3+2πk или x = 2π/3+2πp, где k и p – целые числа. Теперь становится очевидным, что искомое минимальное расстояние между точками и длина дуги находятся между точками с координатами (1/2, π/3) и (–1/2, 2π/3).
Стоит отметить, что отрезок, соединяющий данные точки, параллелен оси абсцисс, то есть его длина равна 1/2 + 1/2 = 1.
Соединим данные точки с началом координат: получим, что центральный угол с вершиной, совпадающей с центром окружности, равен a = π/3, а значит и длина соответствующей дуги равна π/3.
Ответ: длина отрезка равна 1, длина дуги равна π/3.
Похожие вопросы
Предмет: Математика,
автор: sanechka222007
Предмет: Информатика,
автор: hegazyy151
Предмет: Математика,
автор: sanechka222007
Предмет: География,
автор: msdahska1996
Предмет: Литература,
автор: dimitriy95