Question

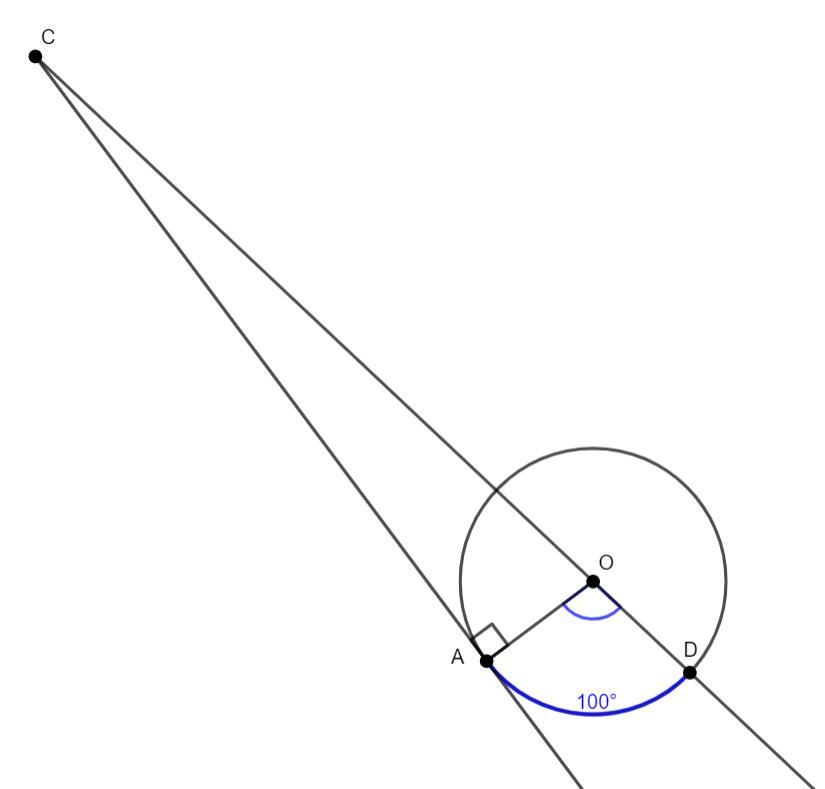
Найдите угол АСО, если его сторона СА касается
окружности, О — центр окружности, а дуга AD
окружности, заключённая внутри этого угла, равна
100градусов

Answer 1

Дано. 

О- центр ок-ти.

АС - касатаельная. 

Дуга АД =100

Решение. 

1.угол ДОА =  дуге АД= 100 гр. (по св-ву центра угла)

2. ОА перпендикулярна АС (по касательной)

3. угол АОС = 180-100= 80 (уг. ДОА и уг. СОА - смежные)

4. Из треуг. АОс: Уг. А +уг. АОС+ уг. АСО = 180(теорема о сумме углов.)

5. уг. АСО = 180-(90+80) = 10. 

ответ: 10.

Answer 2

угол ОАС=90гр, как угол при касательной СА,а угол АСО=10гр. т.к АОД= 100 как центральный, то смежный с ним угол АОС=180-100=80гр. угол АСО=180-(90+80)=10гр.

Answer 3

AO⊥AC, как радиус проведённый в точку касания.

D∈CO ⇒ ∠COD=180°

∠AOD=100°, как центральный угол опирающийся на дугу в 100°.

∠COA=∠COD-∠AOD=180°-100°=80°

Сумма внутренних углов в треугольнике равна 180°, поэтому  в ΔACO:

∠ACO=180°-∠COA-∠OAC=180°-80°-90°=10°

Ответ: 10°.