Предмет: Геометрия,
автор: Клайпеда
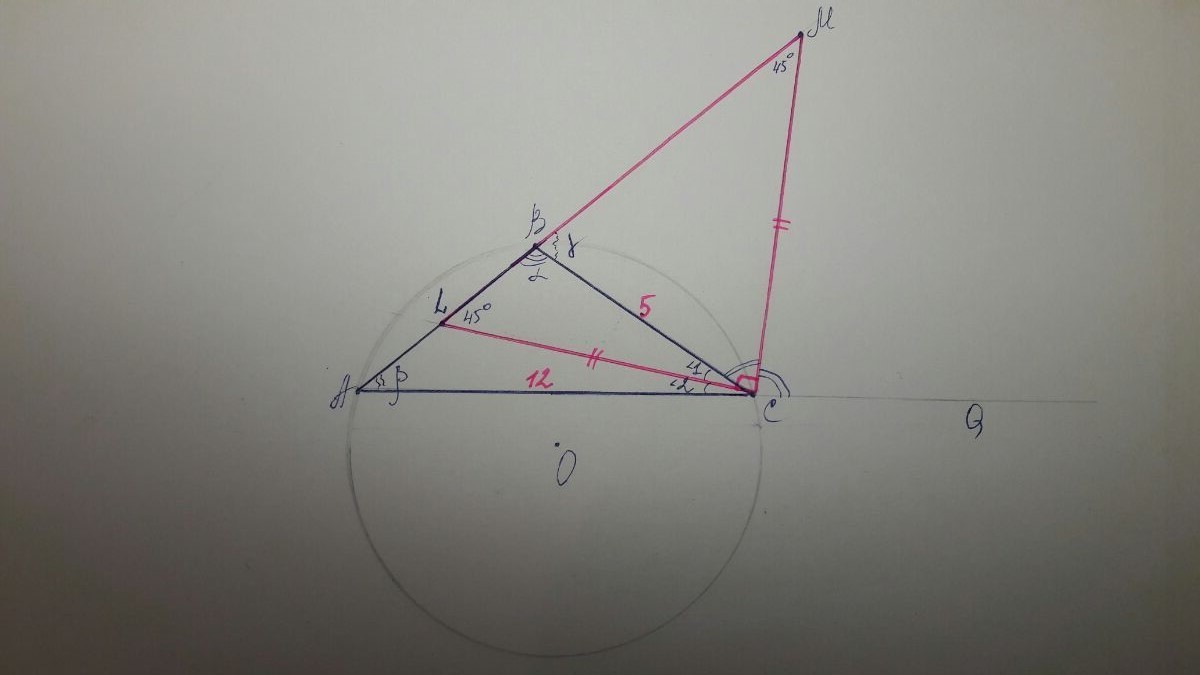
Биссектрисы внутреннего и внешнего углов при вершине С тупоугольного треугольника АВС пересекают прямую АВ в точках L и M соответственно. Найдите радиус окружности, описанной около треугольника АВС, если СL = СМ, ВС = 5, АС = 12.
Ответы
Автор ответа:
0
описана около
Δ
Δ тупоугольный
тупой
и
биссектрисы внутреннего и внешнего углов Δ
∩
∩
?
1)
∩
∩
( по условию)
( по условию)
⇒ Δ
прямоугольный
(по условию) ⇒ Δ
и равнобедренный
2)
Δ
Δ
3)
Δ
⇒
Δ
⇒
⇒
4)
Δ
Ответ:
6.5
рисунок в приложении
Приложения:

Автор ответа:
0
Сейчас я это даже понять не могу. А если когда-нибудь вникну и пойму, то запомнить и объяснить ученикам все равно не смогу.
Автор ответа:
0
Вот еще вариант решения. Поздно увидел задание. http://prntscr.com/ekyr8w
Похожие вопросы
Предмет: Английский язык,
автор: Klarajojo
Предмет: Алгебра,
автор: antonovm
Предмет: Физкультура и спорт,
автор: ahmetkalieva839
Предмет: Математика,
автор: hlfldl44
Предмет: Математика,
автор: ващесвятая