Предмет: Геометрия,
автор: ФильтрВоздуха
Срочно! Нужно на завтрашний день, даю максимальное количество баллов! Задания однотипные, всего четыре штуки! Расписать всё подробно ( с решением, рисунком и дано )
11. В треугольнике ABC известно, что DE — средняя линия. Площадь
треугольника CDE равна 96. Найдите площадь треугольника ABC.
12. В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 20. Найдите площадь треугольника ABC.
13.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
16 В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 21. Найдите площадь треугольника ABC
Ответы
Автор ответа:
0
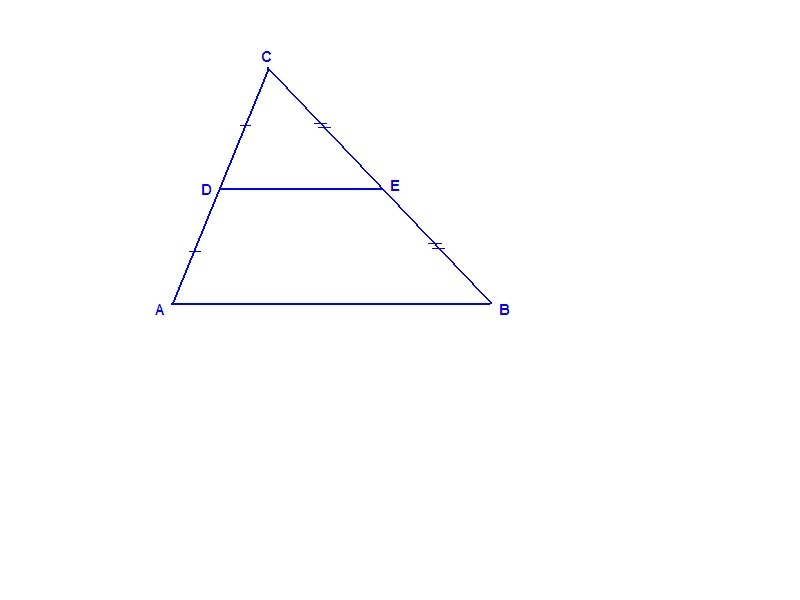
Дано: ΔАВС, DE - средняя линия.
11) Scde = 96
12) Scde = 20
13) Scde = 35
16) Scde = 21.
Найти: Sabc.
Решение:
Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
∠CDE = ∠CAB как соответственные при пересечении параллельных прямых DE и АВ секущей СА,
угол при вершине С общий для треугольников CDE и CAB, значит
ΔCDE подобен ΔCAB по двум углам.
k = CD : CA = 1/2
Отношение площадей подобных треугольников равно квадрату коэффициента подобия:
Scde : Sabc = k² = (1/2)² = 1/4
Sabc = 4 · Scde
11) Sabc = 4 · 96 = 384
12) Sabc = 4 · 20 = 80
13) Sabc = 4 · 35 = 140
16) Sabc = 4 · 21 = 84.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Arinka1308
Предмет: Алгебра,
автор: safarovaazaliya02
Предмет: Алгебра,
автор: MatrixOfsciences
Предмет: Алгебра,
автор: DiannagrantD
Предмет: Литература,
автор: дэнчтк