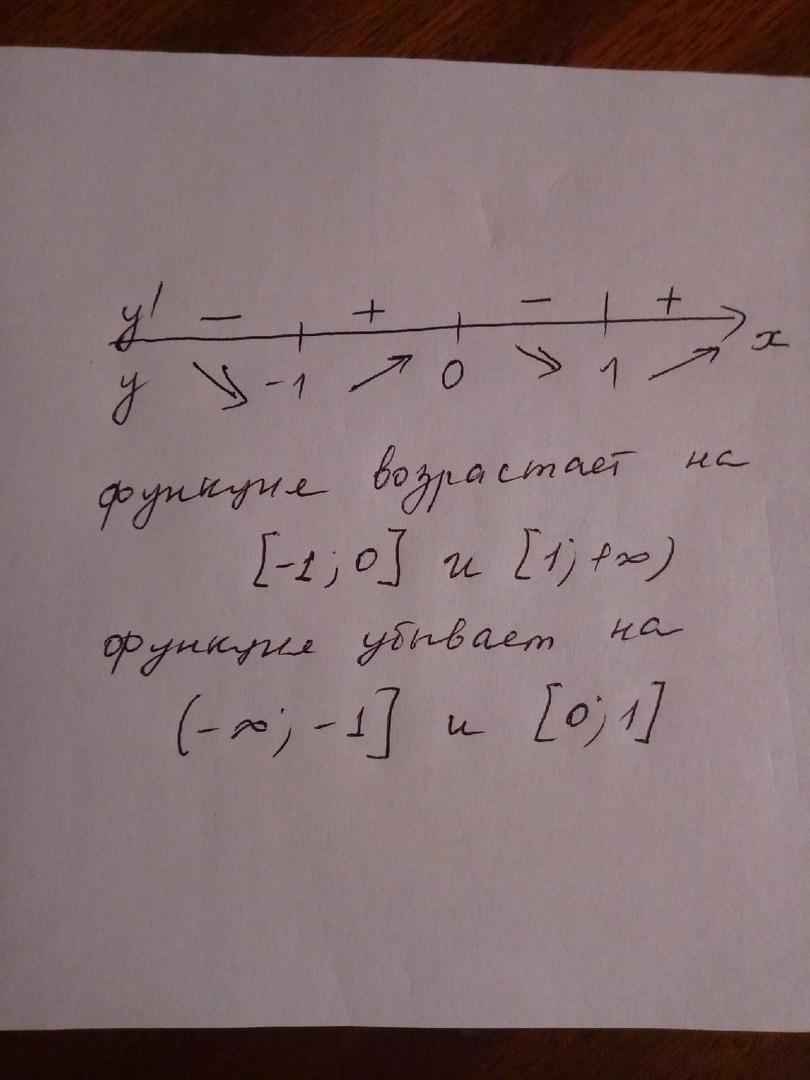Question

1. Найдите промежутки возрастания и убывания функции y=f(x)
а) f(x)=3x–1
б)f(x)=1,5–2x
в)f(x)=x²–6x+5
г) f(x)=x²–4x

2. Найдите промежутки возрастания и убывания функций
а) у=15–2x–х²
в) у=х²–6х
г) у=0,25х⁴–0,5х²–1

Пожалуйста, решите хотя бы одно задание, завтра уже сдавать надо!

Answer 1

Объяснение:

1)

a)

$f(x) =3x -1$

Это линейная функция  и она возрастает  при всех значениях  х , так как угловой коэффициент положителен:  k =3>0

б)

k=-2<0 . Значит линейная функция f(x)=1,5-2x убывает на всей числовой прямой.

в)

$f(x) = x^{2} -6x+5 ;\D(f)=R ;\f' (x) =2x-6;\2x-6=0;\x=3$

На промежутке (-∞ ; 3) производная отрицательна, значит функция убывает на (-∞; 3]

На промежутке  (3; +∞) производная положительна , значит функция возрастает на [3; +∞).

г)

$f(x) =x^{2} -4x;\D(f)=R;\f'(x) =2x-4 ;\2x-4=0;\2x=4;\x=2 .$

На промежутке (-∞ ; 2) производная отрицательна, значит функция убывает на (-∞; 2]

На промежутке  (2; +∞) производная положительна , значит функция возрастает на [2; +∞).

2)

a)

$y=15-2x-x^{2} ;\y' =-2-2x \-2-2x=0;\x=-1$

На промежутке (-1;+∞) производная отрицательна, значит функция убывает на [-1; +∞).

На промежутке  (-∞; -1) производная положительна , значит функция возрастает на (-∞; -1].

в)

$y=x^{2} -6x;\D(y) =R;\y'=2x-6;\2x-6 =0\x=3 .$

На промежутке (-∞ ; 3) производная отрицательна, значит функция убывает на (-∞; 3]

На промежутке  (3; +∞) производная положительна , значит функция возрастает на [3; +∞).

г)

$y= 0,25x^{4} -0,5x^{2} -1 ;\D(y) =R ;\y' = 0,25*4x^{3} -0,5*2x = x^{3} -x =x(x^{2} -1) =x(x-1)(x+1) \y'=0$

Если x=-1,x=0 ,x=1. Продолжение на фото