Предмет: Математика,
автор: kanne1
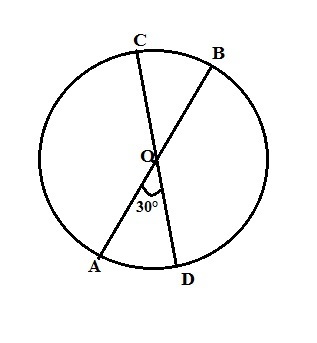
в окружности с центром O проведены диаметры AB и CD. найдите длины дуг на которые делят окружность точки B и D, если известно, AB=8 угол AOD=30°
Ответы
Автор ответа:
0
Диаметр АВ делит своими концами окружность пополам, следовательно, дуга ADB=180°. Центральный угол АОD=30°, значит <DOB=180°-30°=150°.
Итак, точка D делит дугу АDB на два отрезка в отношении AD:DB=1:5.
Дуга ADB=(1/2)*2πR=πR. R=4 (дано). Значит дуга АDB=4π, тогда
дуга DB= (4π/6)*5=(3и1/3)*π (так как AD:DB=1х:5х, а дуга ADB=6x).
Дуга DACB=8π-(3и1/3)π=(4и2/3)π
Если принять π=3, то DB=10, а DACB=14.
Или через формулу длины дуги: L=πR*n/180, где n - центральный угол, опирающийся на эту дугу. В нашем случае центральный угол BOD равен 180°-<AOD или <BOD=180°-30°=150° (так как АВ - диаметр).
Тогда длина дуги BD Lbd=π4*150/180=(3и1/3)*π. Соответственно длина дуги DACB=(4и2/3)π.
Ответ: Точки В и D делят окружность на дуги (при π=3) на
BD=10 и ACBD=14.
Итак, точка D делит дугу АDB на два отрезка в отношении AD:DB=1:5.
Дуга ADB=(1/2)*2πR=πR. R=4 (дано). Значит дуга АDB=4π, тогда
дуга DB= (4π/6)*5=(3и1/3)*π (так как AD:DB=1х:5х, а дуга ADB=6x).
Дуга DACB=8π-(3и1/3)π=(4и2/3)π
Если принять π=3, то DB=10, а DACB=14.
Или через формулу длины дуги: L=πR*n/180, где n - центральный угол, опирающийся на эту дугу. В нашем случае центральный угол BOD равен 180°-<AOD или <BOD=180°-30°=150° (так как АВ - диаметр).
Тогда длина дуги BD Lbd=π4*150/180=(3и1/3)*π. Соответственно длина дуги DACB=(4и2/3)π.
Ответ: Точки В и D делят окружность на дуги (при π=3) на
BD=10 и ACBD=14.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sofkamorkovka1108
Предмет: Биология,
автор: Oksanabakheeva197
Предмет: Алгебра,
автор: Budjagar
Предмет: Обществознание,
автор: Nastyamrs1