Через вершину прямого угла С в равнобедренном треугольнике СДЕ проведена прямая СА, перепендикулярная к плоскости треугольника, СА=35см, СД=12корень из 2. Найдите расстояние от А до прямое ДЕ, найдите тангенс двугранного угла АДЕС.
Если можно, напишите решение как можно быстрее.
Благодарю.
Ответы
Двугранный угол образован двумя плоскостями с общим ребром ( по линии их пересечения). Если провести в каждой плоскости к одной точке ребра двугранного угла перпендикулярные лучи, получим линейный угол двугранного угла, и его величина равна величине данного двугранного угла
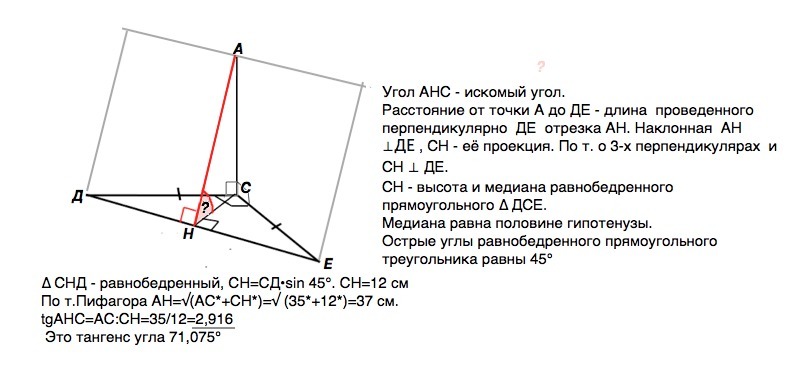
∠ АНС - искомый угол.
Расстояние от точки А до ДЕ - длина проведенного перпендикулярно ДЕ отрезка АН.
АН - наклонная, СН - её проекция. По т. о 3-х перпендикулярах АН и СН перпендикулярны ДЕ.
СН - высота и медиана равнобедренного прямоугольного ∆ ДСЕ.
Медиана прямоугольного треугольника равна половине гипотенузы.
Острые углы равнобедренного прямоугольного треугольника равны 45°
∆ СНД - равнобедренный, СН=СД•sin 45°. СН=12
По т.Пифагора АН=√(АС*+СН*)=√ (35*+12*)=37 см.
tg∠AHC=AC:CH=35/12=2,916
Это тангенс угла 71,075°