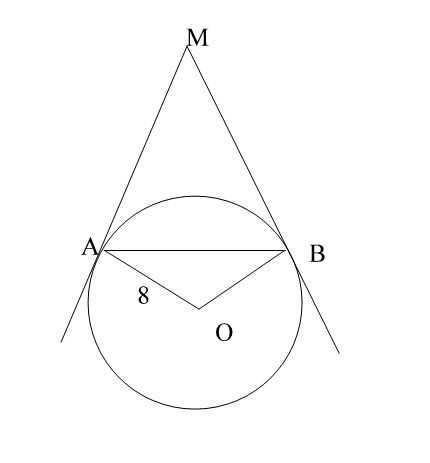
Помогите пожалуйста: 1)Сторона ромба равна 5, меньшая диагональ равна 6.Найдите большую диагональ. 2)Из точки M к окружности с центром О и радиусом 8см проведены касательные АМ и МB(А и B - точки касания).Найдите периметр треугольника ABM , если угол AOB = 120градусов.
Ответы
1. Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам то 62 = 3, по теореме Пифагора 9 + х(квадрат) = 25
Х= 4
4*2 = 8
ответ: 8.
1.
Формула в 1 вложении.
а=5, d=6
D^2 = 4a^2 - d^2
D=8
2.
Ма и Мв-касательные, АВ-секущая.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Т.е. угол МАВ=60 гр. и угол МВА=60 гр. Следовательно, треугольник АМВ-равносторонний.
Проведем из т.О перпендикуляр ОЕ к секущей АВ.
Рассмотрим треугольник АЕО-прямоугольный.
АО=r=8, угол ОЕА=90 гр, угол АОЕ=60 гр, следовательно, угол ОАЕ=30 гр.
Катет, лежащий напротив угла 30 градусов, равен половине гипотенузы.
ОЕ=1/2АО
ОЕ=4
AE^2 = AO^2 - OE^2
АЕ=корень из 48.
АВ=АЕ+ЕВ=2 корня из 48=8 корней из 3.
Р=3*8 корней из 3 = 24 корня из 3.