Question

Из вершины прямого угла С прямоугольного и равнобедренного ΔАВС проведен перпендикуляр СК=4 см к его плоскости. Найти расстояние от точки К до гипотенузы ΔАВС, если АВ=12√2 см.

Если можно, то подробно и с рисунком.

Answer 1

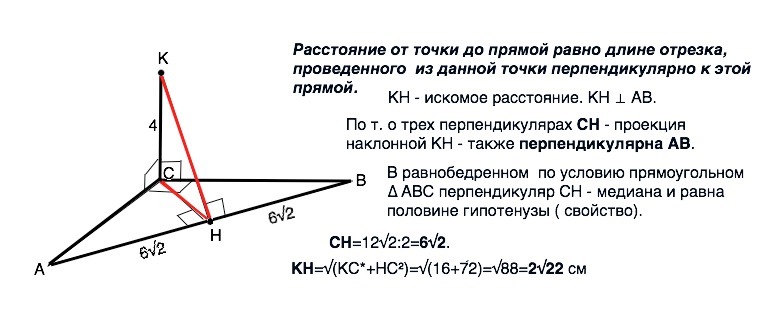
Расстояние от точки до прямой равно длине отрезка, проведенного  из данной точки перпендикулярно к этой прямой. 

КН - искомое расстояние. КН ⊥ АВ. 

По т. о трех перпендикулярах СН - проекция наклонной КН - также перпендикулярна АВ. 

В равнобедренном  по условию прямоугольном ∆ АВС перпендикуляр СН - медиана и равна половине гипотенузы ( свойство). 

СН=12√2:2=6√2.

КН=√(KC*+HC²)=√(16+72)=√88=2√22 см