Question

Решите пожалуйста :) очень надо)

Answer 1

$y=dfrac{-2x^2-10x-15}{x^2+5x+6}$
1. Область определения функции: $x^2+5x+6ne 0,,,, Rightarrow,, (x+2)(x+3)ne 0$
$D(y)=(-infty;-3)cup(-3;3)cup(3;+infty)$

2. Проверим на четность функции:
$y(-x)= dfrac{-2cdot(-x)^2-10cdot (-x)-15}{(-x)^2+5cdot(-x)+6} = dfrac{-(2x^2-10x+15)}{-(-x^2+5x-6)} ne y(x)$
Функция ни четная ни нечетная.

3. Функция непериодическая 

4. Точки пересечения с осью Ох и Оу
   4.1. С осью Ох, это если y=0
$-2x^2-10x-15=0$
Вычислим дискриминант
$D=b^2-4ac=(-10)^2-4cdot(-2)cdot(-15)=-20 textless 0$
Поскольку $D textless 0$, то уравнение действительных корней не имеет.
 4.2. С осью Оу, если это х =0
$y=-2.5$

5. Точки экстремума.
  $y'= dfrac{(-2x^2-10x-15)'(x^2+5x+6)-(-2x^2-10x-15)(x^2+5x+6)'}{(x^2+5x+6)^2} =$

$= dfrac{6x+15}{(x^2+5x+6)^2}$
Приравниваем ее к нулю:
$6x+15=0\ x=-2.5$ - критическая точка

___-__(-3)__-__(-2,5)__+___(-2)__+____
Функция возрастает на промежутке $x in (-2.5;-2)$ и $x in (-2;+infty)$, а убывает на промежутке $xin (-infty;-3)$ и $x in (-3;-2.5)$
В окрестности точки $x=-2.5$ производная функции меняет знак с (-) на (+). Следовательно, точки $x=-2.5$ - точка минимума.

6. Точки перегиба
$y''= dfrac{(6x+15)'(x^2+5x+6)^2-(6x+5)((x^2+5x+6)^2)'}{(x^2+5x+6)^4} =\ \ = dfrac{(x^2+5x+6)(6x^2+30x+36-(12x+10)(2x+5))}{(x^+5x+6)^4} =\ \ =- dfrac{18x^2+90x+114}{(x^2+5x+6)^3}$
Приравниваем к нулю
$- dfrac{18x^2+90x+114}{(x^2+5x+6)^3} =0\ \ 18x^2+90x+114=0\ D=b^2-4ac=90^2-4cdot18cdot 114 textless 0$
Уравнение действительных корней не имеет.

__-___(-3)___+____(-2)__-___
На промежутке $x in (-infty;-3)$ и $(-2;+infty)$ функция выпукла, а на промежутке $x in (-3;-2)$ - вогнута

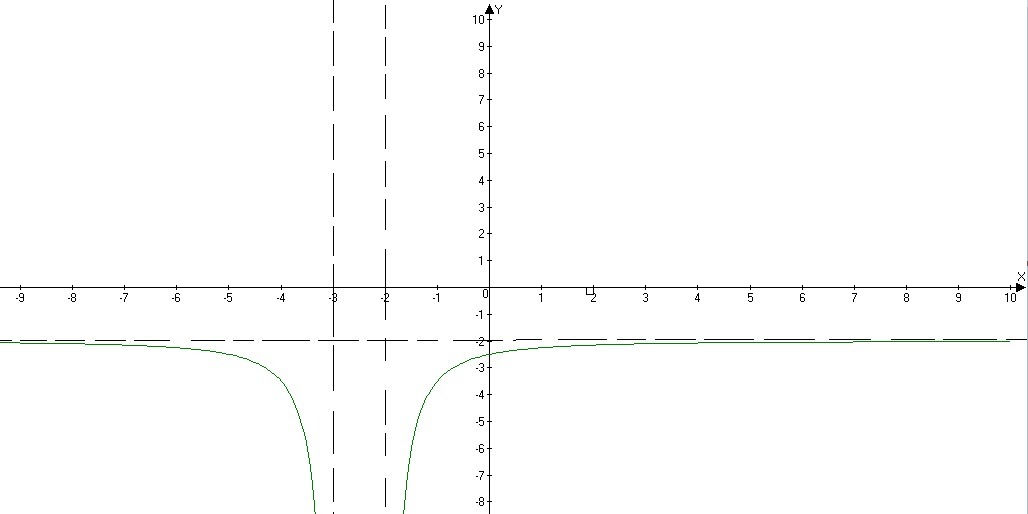
Вертикальные асимптоты: $x=-3;,,,, x=-2$

Горизонтальные асимптоты:
$- dfrac{2x^2+10x+15}{x^2+5x+6} =-2- dfrac{3}{x^2+5x+6} to _{xto infty}-2$

Наклонных асимптот нет.