Question

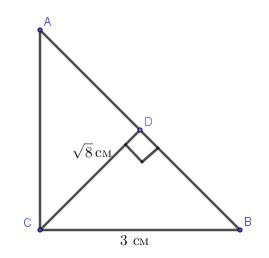
В треугольнике abc изображенном на рисунке известно что угол c=90 градусов cdперпендикулярно ab BC=3 см cd=корень из 8 см найдите длины сторон AC AB BD cos угла b

Answer 1

Из прямоугольного треугольника CDB вычислим BD по теореме Пифагора

$tt BC^2=BD^2+CD^2\ 3^2=BD^2+(sqrt{8} )^2\ 9=BD^2+8\ BD^2=9-8\ BD^2=1\ BD=1~ _{CM}$

• Высота, опущенная из вершины прямого угла на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу

$tt CD^2=ADcdot BD\ \ AD=dfrac{CD^2}{BD}=dfrac{(sqrt{8})^2}{1} =8~_{CM}$

Тогда гипотенуза AB = AD + BD = 8 + 1 = 9 см.

По теореме Пифагора: $tt AC=sqrt{AB^2-BC^2}=sqrt{9^2-3^2} =sqrt{9cdot(9-1)} =3cdot2sqrt{2} =6sqrt{2}$ см.

• Косинус - отношение прилежащего катета к гипотенузе

$tt cosangle B=dfrac{BC}{AB}=dfrac{3}{9} =dfrac{1}{3}$

Ответ: AC = 6√2 см; AB = 9 см; BD = 1 см; cos∠B = 1/3.