Question

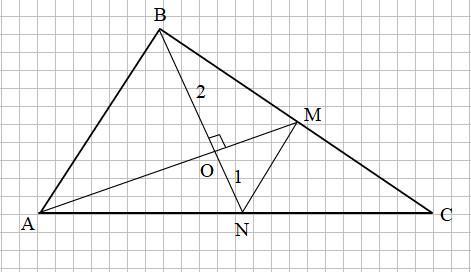
В треугольнике АВС медиана АМ перпендикулярна медиане ВN. Найдите площадь треугольника АВС, если АМ = 2см, ВN = 3см

Answer 1

O - точка пересечения медиан
S(ABC) = S(ABM) + S(AMC)
Медианы в тр-ке делятся в отношении 1 : 2, BO = 2*BN/3
S(ABM) = 0.5*AM*BO = 0.5*AM*(2BN/3) = AM*BN/3
S(AMC) = S(ABM), так как BM=MC, высота, опущенная из А на BC, - общая
S(ABC) = 2*S(ABM) = 2*AM*BN/3 = 4
Ответ: S(ABC) = 4

Answer 2

Ответ:

$S_{ABC}=$ 4см²

Объяснение:

Смотри прикреплённый рисунок.

О - точка пересечения медиан АМ и BN.

Медианы треугольника точкой пересечения О делятся в отношении 2:1, считая от вершины, поэтому BO = $frac{2}{3}BN$= 2 см, NO = $frac{1}{3} BN=$ 1 cм.

Проведём линию MN, соединяющую середины сторон АС и ВС.

MN  = 0.5AB, поскольку MN - средняя линия треугольника.

ΔNMC ~ ΔABC по двум углам (∠С - общий, ∠СMN = ∠СBA как соответственные при MN || AB и секущей ВС)

Коэффициент подобия k = MN: AB = 0,5, поэтому площади ΔNMC и ΔABC относятся, как k² = 0.25.

Тогда площадь трапеции ABMN составляет 0,75 площади ΔABC.

Вычислим площадь трапеции ABMN.

$S_{ABMN} = S_{ABM}+S_{AMN}$.

$S_{ABM} = 0.5cdot AM cdot BO= 0.5cdot 2 cdot 2 = 2(cm^{2} )$

$S_{AMN} = 0.5cdot AM cdot ON= 0.5cdot 2 cdot 1 = 1(cm^{2} )$

$S_{ABMN} = 2 + 1 = 3 (cm^{2} )$

$frac{3}{4}S_{ABC} = 3cm^{2}$.

$S_{ABC} = 4~cm^{2}$.