Question

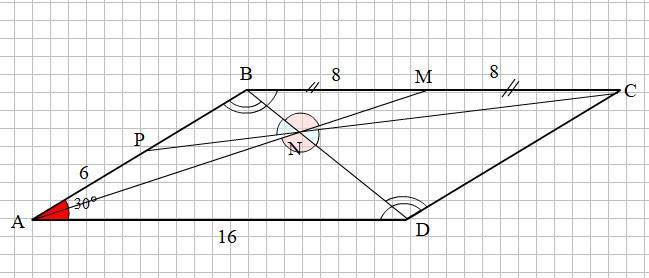
В параллелограмме ABCD угол A=30° AD=16см, M-середина BC. AM пересекает BD в точке N, CN пересекает AB в точке P, AP=6см. Найдите площадь параллелограмма. помогите умолюю бошку сломал

Answer 1

Ответ:

S = 96 см²

Объяснение:

Смотри прикреплённый рисунок.

ΔAND ~ ΔMNB по двум углам (∠BNM = ∠ DNA  как вертикальные; ∠MBN = ∠ADN - накрест лежащие при BM ║ AD и секущей BD).

Тогда BN : ND = BM : AD = 8 : 16 = 1 : 2

ΔBNP ~ ΔDNC по двум углам (∠CND = ∠ BNP как вертикальные; ∠PBN = ∠ CDN - накрест лежащие при ВР ║CD и секущей BD)

Тогда BP : CD = BN : ND = 1 : 2 ⇒ BP = 0.5CD, а поскольку AB = CD как противоположные стороны параллелограмма, то BP = 0.5АВ = АР = 6 см.

Следовательно, АВ = 12 см.

Площадь параллелограмма

S = AB · AD · sin A = 12 · 16 · sin 30° = 12 · 16 · 0.5 = 96 (см²)