Предмет: Геометрия,
автор: Marsbul
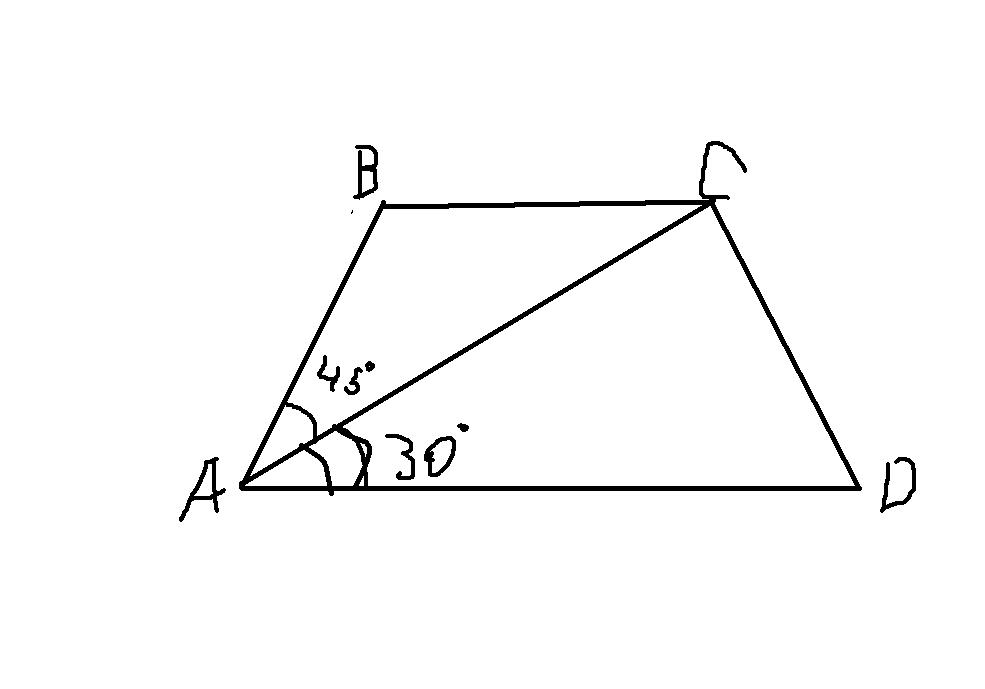
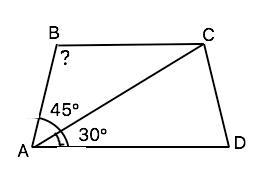
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30 и 45 соответственно
Приложения:
Ответы
Автор ответа:
0
Ответ:105°
Объяснение:
Основания трапеции параллельны, боковые стороны - секущие при них. Сумма внутренних односторонних углов при пересечении параллельных прямых секущей равна 180°. Значит, и сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
∠АВС=180°-(∠ВАС+∠САD)=180°-(45°+30°)=105°.
Углы равнобедренной трапеции, прилежащие к одному основанию, равны. ∠АВС=∠ВСD=105°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: digdaromarov
Предмет: Математика,
автор: nikitamaistruk66
Предмет: Математика,
автор: mansur1235
Предмет: Химия,
автор: mayerkolya
Предмет: Алгебра,
автор: poook