Предмет: Алгебра,
автор: Ernate28
Решите четные задания.
Приложения:

Ответы
Автор ответа:
0
Приложения:
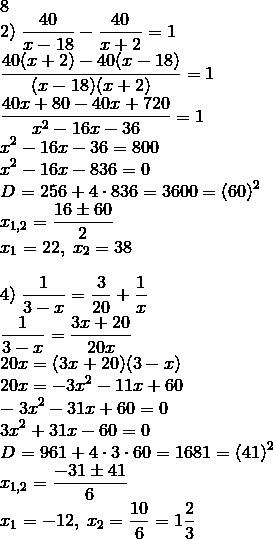
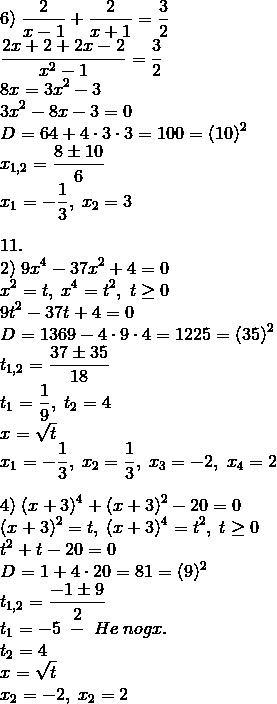
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Русский язык,
автор: kirillk29ks
Предмет: Геометрия,
автор: dimazapreluk
Предмет: Физика,
автор: lerusikrom