Предмет: Математика,
автор: karimturganov
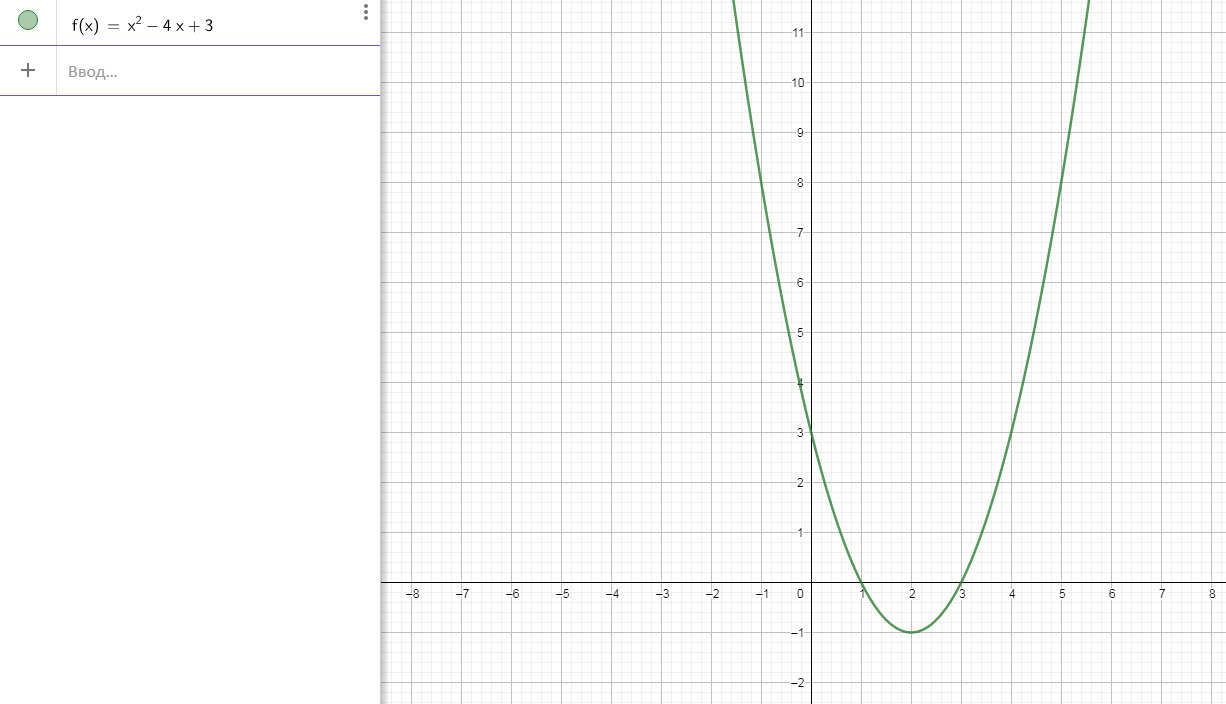
Дана квадратичная функция 1)f(x)=x^2-4x+3 3)f(p)=-3p+4p-5. Для каждой квадратичной функции определите:- при каких значениях аргумента функция обращается в нуль, принимает положительные и отрицательные значения;
-При каком значении аргумента функция имеет наименьшее и наибольшее значение и какое именно
Надеюсь на ответ
Ответы
Автор ответа:
0
См. фото графиков :
1)
Наименьшее значение в точке (2;-1)
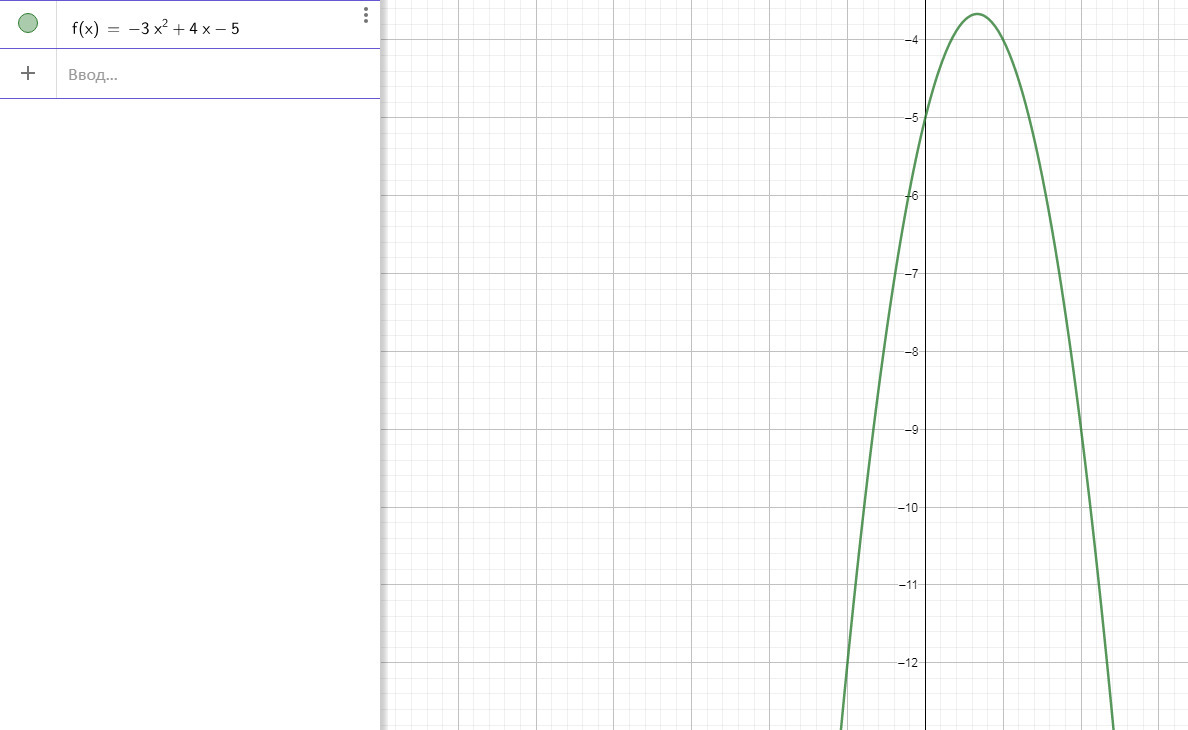
2)
Функция никогда не станет 0
f(p)<0 , x ∈ R
Максимальное значение найдём через производную:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: shokavo64
Предмет: Українська мова,
автор: nazarsova2019
Предмет: Математика,
автор: конак
Предмет: История,
автор: ЛизушаЗайка