Question

Радиус окружности, описанной около правильного треугольника, равен 12 см. Найдите радиус
окружности, вписанной в треугольник.

Answer 1

Ответ:   6 см

Объяснение:

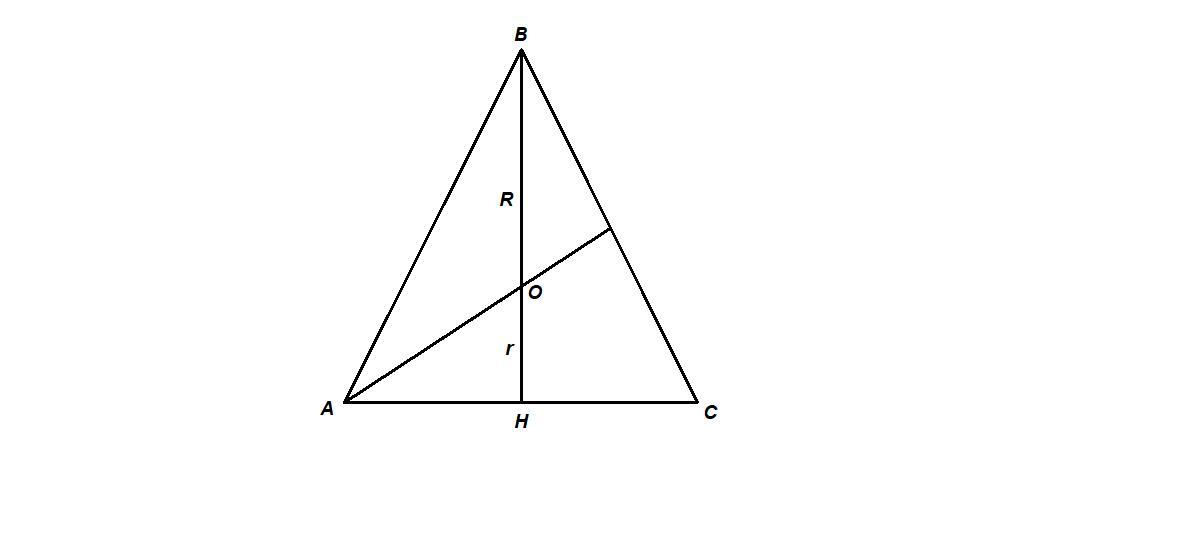
В равностороннем треугольнике любая высота является биссектрисой и медианой, значит центры вписанной и описанной окружностей совпадают.

ОВ = R - радиус описанной окружности

BH = r - радиус вписанной окружности.

Так как точка О - точка пересечения медиан, то она  делит медиану ВН в отношении 2 : 1, считая от вершины, тогда

R : r = 2 : 1

r = 1/2 R = 1/2 · 12 = 6 см