отрезок БД-диаметр окружности с центром О.Хорда АС делит пополам радиус ОБми перпендикулярна к ниму.Найдите углы четырехугольника АБСД и граусные меры дуг АБ БС СД АД
Ответы
Отрезок BД - диаметр окружности с центром О.
Хорда АС делит пополам радиус ОВ и перпендикулярна к нему.
Найдите: углы четырехугольника ABCД и градусные меры дуг AB, BC, CД, AД
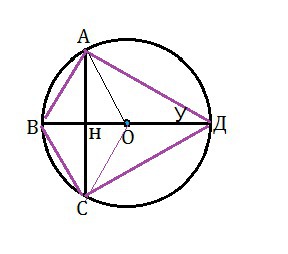
Сделаем и рассмотрим рисунок.
Соединим конец В диаметра и центр О окружности с концом А хорды.
Получим треугольник АВО.
В нем ВО=АО - это радиусы окружности.
ВН=ОН по условию (хорда АС делит пополам радиус ОВ и перпендикулярна к нему).
Отсюда следует, что АН - высота и медиана треугольника АВО, - а это свойство равнобедренного треугольника.⇒ АВ=АО.
АВ=АО=ВО= радиусу окружности. ∆ АВО - равносторонний.
Все углы равностороннего треугольника равны 60°.
На том же основании ∆ ВОС равносторонний с равными углами 60º.
∠ АВС=∠АВО +∠ СВО=120°
Дуга АДВ, на которую опирается угол АВС, вдвое больше и равна 240º. Точка Д диаметра делит эту дугу пополам. ⇒ дуги АД=СД=120°
Четырехугольник АВСД - вписанный,
Известно, что сумма противоположных углов вписанного четырехугольника равна 180°.
Следовательно, ∠ АДС =180°-∠АВС= 180°-120°=60°
Вписанные углы ВАД и ВСД опираются дуги, стягиваемые диаметром.
Диаметр делит окружность пополам и стягивает дугу 180º
Вписанный угол, опирающийся на диаметр, равен половине дуги, на которую опирается, и равен 180º:2=90°
Ответ: ∠А=∠С=90°
∠В=120º, ∠Д=60º
Дуги АВ=ВС=60°, дуги СД=АД=120º